
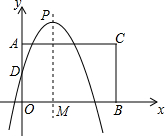
 ��ͼ����ƽ��ֱ������ϵ�У���A��B�ֱ���y�������ᣬx���������������㣬OA=2k��OB=2k+3����AO��BOΪ�ڱ߹������AOBC��������y=-$\frac{3}{4}$x2+3x+k��y���ڵ�D��PΪ���㣬PM��x���ڵ�M��
��ͼ����ƽ��ֱ������ϵ�У���A��B�ֱ���y�������ᣬx���������������㣬OA=2k��OB=2k+3����AO��BOΪ�ڱ߹������AOBC��������y=-$\frac{3}{4}$x2+3x+k��y���ڵ�D��PΪ���㣬PM��x���ڵ�M������ ��1����D��y=-$\frac{3}{4}$x2+3x+k�ϣ�����y���ϣ���y=0�����D���꣬���������߶��㹫ʽ��������ɣ�
��2������k��ʾ����صĵ�����꣬����PM=BM�������̼��ɣ�
��3��������k��ʾ����صĵ�����꣬���ݡ�ADP�ǵ��������Σ������������AD=AP��DA=DP��PA=PD���㣻
���ɵ�P��D�������ֱ��PD����ʽ������PD��AA�䣬��A��0��2k����ȷ����AA�����ʽ���̶�������㣬�����A������꼴�ɣ�
��� �⣺��1����x=0������$y=-\frac{3}{4}{x^2}+3x+k$��
��y=k��
��OD=k��
��$\frac{{4ac-{b^2}}}{4a}=\frac{{4����-\frac{3}{4}����k-{3^2}}}{{4����-\frac{3}{4}��}}=k+3$��
��PM=k+3��
��2����$-\frac{b}{2a}=-\frac{3}{{2����-\frac{3}{4}��}}=2$��
��OM=2��BM=OB-OM=2k+3-2=2k+1��
�֡�PM=k+3��PM=BM��
��k+3=2k+1��
���k=2��
��������ߵı���ʽΪ$y=-\frac{3}{4}{x^2}+3x+2$��
��3����
����P�ھ���AOBC�ⲿʱ
��ͼ1��
��P��PK��OA�ڵ�K����AD=APʱ��
��AD=AO-DO=2k-k=k��
��AD=AP=k��KA=KO-AO=PM-AO=k+3-2k=3-k
KP=OM=2����Rt��KAP��KA2+KP2=AP2
�ࣨ3-k��2+22=k2�����$k=\frac{13}{6}$��
����P�ھ���AOBC�ڲ�ʱ
��PD=APʱ����P��PH��OA��H��
AD=k��HD=$\frac{k}{2}$��$HO=DO+HD=\frac{3k}{2}$
�֡�HO=PM=k+3��
��$\frac{3k}{2}=k+3$��
���k=6��
��DP=DAʱ����D��PQ��PM��Q��
PQ=PM-QM=PM-OD=k+3-k=3
DQ=OM=2��DP=DA=k��
��Rt��DQP��$DP=\sqrt{D{Q^2}+Q{P^2}}=\sqrt{{2^2}+{3^2}}=\sqrt{13}$��
��$k=DP=\sqrt{13}$��
����$k=\frac{13}{6}$��k=6��k=$\sqrt{13}$��
�ڡ�P��2��k+3����D��0��k��
��ֱ��PD����ʽΪy=$\frac{3}{2}$x+k��
��A��0��2k����
��ֱ��AA��Ľ���ʽΪy=-$\frac{2}{3}$x+2k��
��ֱ��PD��ֱ��AA��Ľ���Ϊ��$\frac{6}{13}$k��$\frac{22}{13}$k����
��A�䣨$\frac{12}{13}$k��$\frac{18}{13}$k����
��A����������y=-$\frac{3}{4}$x2+3x+k�ϣ�
��-$\frac{3}{4}$����$\frac{12}{13}$k��2+3��$\frac{12}{13}$k+k=$\frac{18}{13}$k��
��k=$\frac{403}{108}$��k=0���ᣩ
���� �����Ƕ��κ����ۺ��⣬��Ҫ�����˶��κ�������ʽ��ȷ����ƽ������ϵ�����߶εij������������ε����ʣ�ȷ������������ʽ�ǽⱾ��Ĺؼ����⣨3���DZ�����ѵ㣮


 ���Ǽ���С����ϵ�д�
���Ǽ���С����ϵ�д� �Ͻ�ƽ���Ȿϵ�д�
�Ͻ�ƽ���Ȿϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ����ͼ���ھ���ABCD�У�BC=6��CD=3������BCD�ضԽ���BD���ۣ���C���ڵ�C�䴦��BC�佻AD�ڵ�E�����߶�DE�ij�Ϊ3.75��
����ͼ���ھ���ABCD�У�BC=6��CD=3������BCD�ضԽ���BD���ۣ���C���ڵ�C�䴦��BC�佻AD�ڵ�E�����߶�DE�ij�Ϊ3.75���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
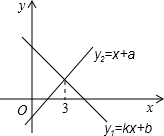 һ�κ���y1=kx+b��y2=x+a��ͼ����ͼ�������x�IJ���ʽkx+b��x+a�Ľ⼯��x��3��
һ�κ���y1=kx+b��y2=x+a��ͼ����ͼ�������x�IJ���ʽkx+b��x+a�Ľ⼯��x��3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ������C1��y=a��x+1����x-3a����a��0����x�ύ��A��B���㣨A��B����ࣩ����y�ύ�ڵ�C��0��-3����
������C1��y=a��x+1����x-3a����a��0����x�ύ��A��B���㣨A��B����ࣩ����y�ύ�ڵ�C��0��-3�����鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com