
 如下图,在矩形ABCD中,BC=6,CD=3,将△BCD沿对角线BD翻折,点C落在点C′处,BC′交AD于点E,则线段DE的长为3.75.
如下图,在矩形ABCD中,BC=6,CD=3,将△BCD沿对角线BD翻折,点C落在点C′处,BC′交AD于点E,则线段DE的长为3.75. 科目:初中数学 来源: 题型:解答题
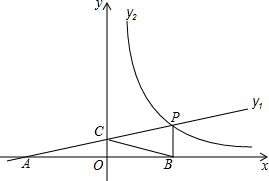 如图所示,直线y1=$\frac{1}{4}x+1$与x轴交于点A,与y轴交于点C,与反比例函数y2=$\frac{m}{x}$(x>0)的图象交于点P,作PB⊥x轴于点B,且AC=BC.
如图所示,直线y1=$\frac{1}{4}x+1$与x轴交于点A,与y轴交于点C,与反比例函数y2=$\frac{m}{x}$(x>0)的图象交于点P,作PB⊥x轴于点B,且AC=BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 2016年2月18日韩国海军海警在朝鲜半岛东部海域实施联合演习,在返回济州岛军事基地途中,韩国海军UH-60直升机在距海平面垂直高度为300米的点C处测得济州一小岛的西端点A的俯角为60°,然后沿着平行于AB的方向水平飞行了3500米,在点D测得这小岛的东端点B的俯角为45°,求这个济州小岛东西两端BA的距离(结果精确到1米,参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)
2016年2月18日韩国海军海警在朝鲜半岛东部海域实施联合演习,在返回济州岛军事基地途中,韩国海军UH-60直升机在距海平面垂直高度为300米的点C处测得济州一小岛的西端点A的俯角为60°,然后沿着平行于AB的方向水平飞行了3500米,在点D测得这小岛的东端点B的俯角为45°,求这个济州小岛东西两端BA的距离(结果精确到1米,参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
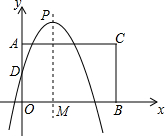 如图,在平面直角坐标系中,点A,B分别是y轴正半轴,x轴正半轴上两动点,OA=2k,OB=2k+3,以AO,BO为邻边构造矩形AOBC,抛物线y=-$\frac{3}{4}$x2+3x+k交y轴于点D,P为顶点,PM⊥x轴于点M.
如图,在平面直角坐标系中,点A,B分别是y轴正半轴,x轴正半轴上两动点,OA=2k,OB=2k+3,以AO,BO为邻边构造矩形AOBC,抛物线y=-$\frac{3}{4}$x2+3x+k交y轴于点D,P为顶点,PM⊥x轴于点M.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 12 | B. | 15 | C. | 18 | D. | 21 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
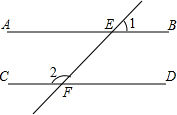 如图,AB∥CD,直线EF分别交直线AB,CD于点E,F,若∠1=46°,则∠2的度数为( )
如图,AB∥CD,直线EF分别交直线AB,CD于点E,F,若∠1=46°,则∠2的度数为( )| A. | 44° | B. | 46° | C. | 134° | D. | 144° |
查看答案和解析>>
科目:初中数学 来源:2017届四川省广安市岳池县九年级第二次诊断考试数学试卷(解析版) 题型:解答题
(14分) 某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)请直接写出y与x的函数关系式;
(2)当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?
(3)设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com