
【题目】已知关于x的一元二次方程2x2+(a+4)x+a=0.
(1)求证:无论a为任何实数,此方程总有两个不相等的实数根;
(2)抛物线![]() 与x轴的一个交点的横坐标为
与x轴的一个交点的横坐标为![]() ,其中a≠0,将抛物线C1向右平移
,其中a≠0,将抛物线C1向右平移![]() 个单位,再向上平移
个单位,再向上平移![]() 个单位,得到抛物线C2.求抛物线C2的解析式;
个单位,得到抛物线C2.求抛物线C2的解析式;
(3)点A(m,n)和B(n,m)都在(2)中抛物线C2上,且A、B两点不重合,求代数式2m3﹣2mn+2n3的值.
【答案】(1)见解析;(2)y=2x2﹣3.(3)![]() .
.
【解析】
试题分析:(1)先求出判别式的值,根据△>0时,方程有两个不相等的实数根,即可得出结论;
(2)将点(![]() ,0)代入抛物线C1解析式,得出a的值,从而确定C1解析式,根据平移的规律可得出抛物线C2的解析式;
,0)代入抛物线C1解析式,得出a的值,从而确定C1解析式,根据平移的规律可得出抛物线C2的解析式;
(3)将点A(m,n)和B(n,m)代入抛物线C2的解析式,通过整理、化简可得出代数式2m3﹣2mn+2n3的值.
(1)证明:∵△=(a+4)2﹣4×2a=a2+16,
而a2≥0,
∴a2+16>0,即△>0.
∴无论a为任何实数,此方程总有两个不相等的实数根.
(2)∵当![]() 时,y=0,
时,y=0,
∴2×(![]() )2+(a+4)×
)2+(a+4)×![]() +a=0,
+a=0,
∴a2+3a=0,即a(a+3)=0,
∵a≠0,
∴a=﹣3.
∴抛物线C1的解析式为y=2x2+x﹣3=2(x+![]() )2﹣
)2﹣![]() ,
,
∴抛物线C1的顶点为(﹣![]() ,﹣
,﹣![]() ),
),
∴抛物线C2的顶点为(0,﹣3).
∴抛物线C2的解析式为y=2x2﹣3.
(3)∵点A(m,n)和B(n,m)都在抛物线C2上,
∴n=2m2﹣3,m=2n2﹣3,
∴n﹣m=2(m2﹣n2),
∴n﹣m=2(m﹣n)(m+n),
∴(m﹣n)[2(m+n)+1]=0,
∵A、B两点不重合,即m≠n,
∴2(m+n)+1=0,
∴m+n=﹣![]() ,
,
∵2m2=n+3,2n2=m+3,
∴2m3﹣2mn+2n3=2m2m﹣2mn+2n2n=(n+3)m﹣2mn+(m+3)n=3(m+n)=![]() .
.


科目:初中数学 来源: 题型:
【题目】2014年8月26日,第二届青奥会在南京举行,甲、乙、丙、丁四位跨栏运动员在为该运动会积极准备.在某天“110米跨栏”训练中,每人各跑5次,据统计,他们的平均成绩都是13.2秒,甲、乙、丙、丁的成绩的方差分别是0.11,0.03,0.05,0.02.则当天这四位运动员“110米跨栏”的训练成绩最稳定的是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中,E为BC中点,作∠AEC的角平分线交AD于F点.若AB=6,AD=16,则FD的长度为何?( )
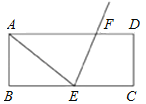
A.4 B.5 C.6 D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农场去年种植南瓜10亩,亩产量为2000kg,今年该农场扩大了种植面积,并引进新品种,使总产量增长到60000kg.已知今年种植面积的增长率是今年平均亩产量增长率的2倍,求今年平均亩产量的增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,对于平面内任一点(a,b),若规定以下三种变换:①△(a,b)=(-a,b);②○(a,b)=(-a,-b);③□(a,b)=(a,-b).按照以上变换,例如:△(○(1,2))=(1,-2),则○(□(3,4))=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E在AD上,EC平分∠BED.
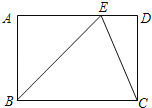
(1)△BEC是否为等腰三角形?为什么?
(2)若AB=a,∠ABE=45°,求BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com