
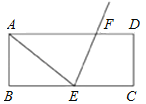
【题目】如图,长方形ABCD中,E为BC中点,作∠AEC的角平分线交AD于F点.若AB=6,AD=16,则FD的长度为何?( )
A.4 B.5 C.6 D.8
【答案】C
【解析】
试题分析:首先由矩形ABCD的性质,得BC=AD=16,已知E为BC中点,则BE=BC÷2=8,根据勾股定理在直角三角形ABE中可求出AE,再由∠AEC的角平分线交AD于F点,得∠AEF=∠CEF,已知矩形ABCD,AD∥BC,
则∠AFE=∠CEF,所以∠AEF=∠AFE,所以AF=AE,从而求出FD.
解:已知矩形ABCD,∴BC=AD=16,
又E为BC中点,
∴BE=![]() ×BC=
×BC=![]() ×16=8,
×16=8,
在直角三角形ABE中,
AE2=AB2+BE2=62+82=100,
∴AE=10,
已知矩形ABCD,
∴AD∥BC,
∴∠AFE=∠CEF,
又∠AEC的角平分线交AD于F点,
∴∠AEF=∠CEF,
∴∠AEF=∠AFE,
∴AF=AE=10,
∴FD=AD﹣AF=16﹣10=6,
故选:C.


科目:初中数学 来源: 题型:
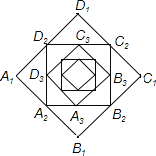
【题目】如图,小宋作出了边长为2的第一个正方形A1B1C1D1,算出了它的面积.然后分别取正方形A1B1C1D1四边的中点A2、B2、C2、D2作出了第二个正方形A2B2C2D2,算出了它的面积.用同样的方法,作出了第三个正方形A3B3C3D3,算出了它的面积…,由此可得,第六个正方形A6B6C6D6的面积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程2x2+(a+4)x+a=0.
(1)求证:无论a为任何实数,此方程总有两个不相等的实数根;
(2)抛物线![]() 与x轴的一个交点的横坐标为
与x轴的一个交点的横坐标为![]() ,其中a≠0,将抛物线C1向右平移
,其中a≠0,将抛物线C1向右平移![]() 个单位,再向上平移
个单位,再向上平移![]() 个单位,得到抛物线C2.求抛物线C2的解析式;
个单位,得到抛物线C2.求抛物线C2的解析式;
(3)点A(m,n)和B(n,m)都在(2)中抛物线C2上,且A、B两点不重合,求代数式2m3﹣2mn+2n3的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“石头、剪刀、布”是民间广为流传的游戏,游戏时,双方每次只能做“石头”、“剪刀”、“布”这三种手势中的一种.假定双方每次都是等可能的做这三种手势.
问:小强和小刚在一次游戏时,
(1)两个人同时出现“石头”手势的概率是多少?
(2)两个人出现不同手势的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市一月份的营业额为200万元,已知第一季度的总营业额共1000万元,如果平均每月增长率为x,则由题意列方程应为( )
A.200(1+x)2=1000
B.200+200×2x=1000
C.200+200×3x=1000
D.200[1+(1+x)+(1+x)2]=1000
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com