
分析 (1)直接根据给出的式字规律即可得出结论;
(2)根据题中给出的例子进行计算即可.
解答 解:(1)∵$\frac{1}{1×3}$=$\frac{1}{2}$×(1-$\frac{1}{3}$),$\frac{1}{3×5}$=$\frac{1}{2}$×($\frac{1}{3}$-$\frac{1}{5}$),$\frac{1}{5×7}$=$\frac{1}{2}$($\frac{1}{5}$-$\frac{1}{7}$)…
∴$\frac{1}{n(n+2)}$=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+2}$).
故答案为:$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+2}$);
(2)原式=$\frac{1}{2}$(1-$\frac{1}{3}$)+$\frac{1}{2}$($\frac{1}{2}$-$\frac{1}{4}$)+$\frac{1}{2}$($\frac{1}{3}$-$\frac{1}{5}$)+…+$\frac{1}{2}$($\frac{1}{2011}$-$\frac{1}{2013}$)+$\frac{1}{2}$($\frac{1}{2012}$-$\frac{1}{2014}$)+$\frac{1}{2}$($\frac{1}{2013}$-$\frac{1}{2015}$)
=$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{2}$-$\frac{1}{4}$+$\frac{1}{3}$-$\frac{1}{5}$+…+$\frac{1}{2011}$-$\frac{1}{2013}$+$\frac{1}{2012}$-$\frac{1}{2014}$+$\frac{1}{2013}$-$\frac{1}{2015}$)
=$\frac{1}{2}$×(1+$\frac{1}{2}$-$\frac{1}{2014}$-$\frac{1}{2015}$)
=$\frac{3041643}{4058210}$.
点评 本题考查了有理数的混合运算、规律型-数字的变化类,弄清题意,得出一般性的规律是解本题的关键.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:解答题
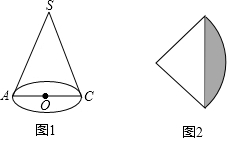 如图1,圆锥底面圆半径为1,母线长为4,图2为其侧面展开图.
如图1,圆锥底面圆半径为1,母线长为4,图2为其侧面展开图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
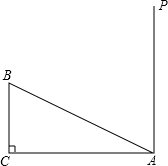 如图,在Rt△ABC中,∠C=90°,AC=16,BC=8,MN=AB,点M、N分别在AC和过点A且垂直于AC的射线AP上运动,问:点M运动到什么位置时,△ABC和以A、M、N为顶点的三角形全等(画出图形,写出解答过程).
如图,在Rt△ABC中,∠C=90°,AC=16,BC=8,MN=AB,点M、N分别在AC和过点A且垂直于AC的射线AP上运动,问:点M运动到什么位置时,△ABC和以A、M、N为顶点的三角形全等(画出图形,写出解答过程).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
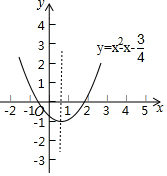 如图,根据函数y=x2-x-$\frac{3}{4}$的图象填空:
如图,根据函数y=x2-x-$\frac{3}{4}$的图象填空:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
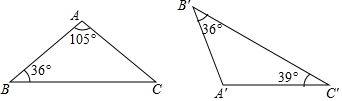 具备下列各组条件的两个三角形中,不一定相似的是( )
具备下列各组条件的两个三角形中,不一定相似的是( )| A. | 有一个角是36°的两个等腰三角形 | |
| B. | 有一个角为108°的两个等腰三角形 | |
| C. | 有一锐角对应相等的两个直角三角形 | |
| D. | 图中的△ABC与△A'B'C'相似 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
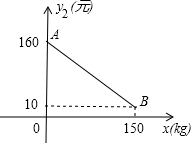 某加工企业生产并销售某种农产品,假设销售量与加工产量相等.已知每千克生产成本y1(单位:元)与产量x(单位:kg)之间满足关系式y1=$\left\{\begin{array}{l}{-0.5x+100(0≤x<80)}\\{3x-180(80≤x≤150)}\end{array}\right.$.如图中线段AB表示每千克销售价格y2(单位:元)与产量x(单位:kg)之间的函数关系式.
某加工企业生产并销售某种农产品,假设销售量与加工产量相等.已知每千克生产成本y1(单位:元)与产量x(单位:kg)之间满足关系式y1=$\left\{\begin{array}{l}{-0.5x+100(0≤x<80)}\\{3x-180(80≤x≤150)}\end{array}\right.$.如图中线段AB表示每千克销售价格y2(单位:元)与产量x(单位:kg)之间的函数关系式.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com