
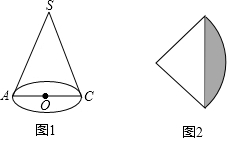
 如图1,圆锥底面圆半径为1,母线长为4,图2为其侧面展开图.
如图1,圆锥底面圆半径为1,母线长为4,图2为其侧面展开图.分析 (1)如图2中,作SE⊥AF交弧AF于C.设图2中的扇形的圆心角为n°,由题意$\frac{nπ•4}{180}$=2π•1,求出n即可解决问题.
(2)在图2中,根据垂线段最短求出AE,即为最短的长度.
解答 解:(1)如图2中,作SE⊥AF交弧AF于C.
设图2中的扇形的圆心角为n°,
由题意$\frac{nπ•4}{180}$=2π•1,
∴n=90°,
∵SA=SF,
∴△SFA是等腰直角三角形,
∴SE=$\frac{1}{2}$AF=$\frac{1}{2}$×$4\sqrt{2}$=2$\sqrt{2}$,
∴S阴=S扇形S-AF-S△SAF=$\frac{90π•{4}^{2}}{360}$-$\frac{1}{2}$×$4\sqrt{2}$×$2\sqrt{2}$=4π-8.
(2)在图2中,∵SC是一条蜜糖线,AE⊥SC,AE=2$\sqrt{2}$,
∴根据垂线段最短,一只蚂蚁从A沿着圆锥表面最少需要爬2$\sqrt{2}$个单位长度才能吃到蜜糖.
点评 本题考查圆锥的侧面展开图、弧长公式、扇形面积公式、垂线段最短等知识,解题的关键是灵活运用这些公式解决问题,学会利用参数,构建方程解决问题,属于中考常考题型.


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com