
分析 (1)先去括号再合并同类项即可解答本题;
(2)根据幂的乘方和同底数幂的乘法可以解答本题;
(3)根据幂的乘方和同底数幂的乘法、合并同类项可以解答本题;
(4)根据幂的乘方和单项式乘以多项式可以解答本题;
(5)根据幂的乘方可以解答本题;
(6)根据幂的乘方和同底数幂的乘法可以解答本题;
(7)先对题目中的式子化简,再将x的代入即可解答本题.
解答 解:(1)$\frac{1}{4}$m-$\frac{1}{2}$n+2(-m+3n)
=$\frac{1}{4}m-\frac{1}{2}n-2m+6n$
=$-\frac{7}{4}m+\frac{11}{2}n$;
(2)x3•(-x)5•(x2)3
=x3•(-x5)•x6
=-x14;
(3)(-2x3)2-(3x3)3-(2x)2(2x4)
=4x6-27x9-4x2•2x4
=4x6-27x9-8x6
=-4x6+27x9;
(4)(-$\frac{1}{2}$xy2)2(3xy-4xy2+1)
=$\frac{1}{4}{x}^{2}{y}^{4}$(3xy-4xy2+1)
=$\frac{3}{4}{x}^{3}{y}^{5}$-x3y6+$\frac{1}{4}{x}^{2}{y}^{4}$;
(5)(-3)5×(-$\frac{2}{3}$)5×56
=$(-3)^{5}×\frac{{2}^{5}}{(-3)^{5}}×{5}^{6}$
=500000;
(6)(-$\frac{1}{2}$×103)2(4×102)3
=$\frac{1}{4}×1{0}^{6}×{4}^{3}×1{0}^{6}$
=1.6×1013;
(7)∵A=2x2-3x-1,B=-$\frac{1}{2}$x+4x2-3,C=x(-2x-1),
∴A-2B+C
=2x2-3x-1-2(-$\frac{1}{2}$x+4x2-3)+x(-2x-1)
=2x2-3x-1+x-8x2+6-2x2-x
=-8x2-3x+5,
当x=-2时,原式=-8×(-2)2-3×(-2)+5=-21.
点评 本题考查整式的混合运算-化简求值,解题的关键是明确整式的混合运算的计算方法.


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:初中数学 来源: 题型:解答题
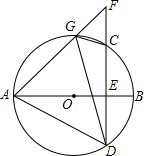 如图,AB是圆O的直径,弦CD⊥AB于点E,G是$\widehat{AC}$上任意一点,连结AD,GD,GC,延长AG、DC交于点F.
如图,AB是圆O的直径,弦CD⊥AB于点E,G是$\widehat{AC}$上任意一点,连结AD,GD,GC,延长AG、DC交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
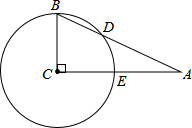 如图,在△ABC中,∠C=90°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E.
如图,在△ABC中,∠C=90°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
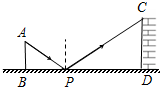 如图,是小李设计用手电来测量某古城墙高度的示意图,点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.1米,BP=1.9米,PD=19米,那么该古城墙CD的高度是11米.
如图,是小李设计用手电来测量某古城墙高度的示意图,点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.1米,BP=1.9米,PD=19米,那么该古城墙CD的高度是11米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
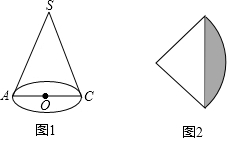 如图1,圆锥底面圆半径为1,母线长为4,图2为其侧面展开图.
如图1,圆锥底面圆半径为1,母线长为4,图2为其侧面展开图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com