
分析 (1)观察题目所给等式,总结隐含的恒等变换,直接写出所求等式.
(2)利用等式:$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$将相邻两个正整数的积的倒数写成它们的倒数的差,然后计算出结果即可.
解答 解:(1)∵$\frac{1}{n}$-$\frac{1}{n+1}$=$\frac{n+1}{n(n+1)}$-$\frac{n}{n(n+1)}$=$\frac{1}{n(n+1)}$
∴$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$
(2)①$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2006×2007}$
=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{2006}$-$\frac{1}{2007}$
=1-$\frac{1}{2007}$
=$\frac{2006}{2007}$
②$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{n(n+1)}$
=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$
=1-$\frac{1}{n+1}$
=$\frac{n}{n+1}$
故答案为:(1)$\frac{1}{n}$-$\frac{1}{n+1}$;(2)①$\frac{2006}{2007}$;②$\frac{n}{n+1}$
点评 本题考查了数字的变化规律问题,解题的关键是能够总结出题目隐含的数字变换规律并加以运用


 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
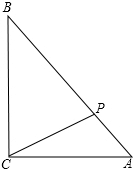 如图所示,在R△ABC中,∠C=90°,AC=6,AB=10,点P为AB上一点,设PB=x,△ACP的面积为y,写出y与x之间的函数关系式及x的取值范围.
如图所示,在R△ABC中,∠C=90°,AC=6,AB=10,点P为AB上一点,设PB=x,△ACP的面积为y,写出y与x之间的函数关系式及x的取值范围.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com