
 ��ͼ����֪������y=ax2+bx+c��x�����������A��B����ֱ�Ϊ��-1��0������-3��0������������y�ύ��CΪ��0��3����
��ͼ����֪������y=ax2+bx+c��x�����������A��B����ֱ�Ϊ��-1��0������-3��0������������y�ύ��CΪ��0��3�������� ��1�����ݴ���ϵ�������ɵú�������ʽ�������䷽�����ɵö������ꣻ
��2���ٸ����߶δ�ֱƽ�����ϵĵ㵽�߶����˵�ľ�����ȣ�����֮���߶���̣��ɵ�P�ڶԳ�����BC�Ľ��㣬�����Ա����뺯��ֵ�Ķ�Ӧ��ϵ���ɵ�P�����꣬���������ľ��룬�ɵô𰸣�
�ڸ���PA=AC���ɵ�P�����꣬��������֮��ľ��룬�ɵ�t��ֵ������PC=AC���ɵ�P�����꣬��������֮��ľ��룬�ɵ�t��ֵ��
�۸������������ε��ж������ʣ��ɵù���m�ķ��̣����ݽⷽ�̣��ɵô𰸣�
��� �⣺��1���������߽���ʽΪy=a��x+1����x+3��
�ѣ�0��3�������
a��0+1����0+3��=3
a=1��
��y=��x+1����x+3��=x2+4x+3
�֡�y=��x+2��2-1
��D��-2��-1����
��2����ͼ1��
��P�������߶Գ�����һ����
����PAC�ܳ���Сʱ����PA+PCֵ��С��
�����·���ɵã���A��B���ڶԳ���Գ�
��ֱ��BC��Գ��ύ�㼴ΪP��
��ֱ��BC����ʽΪy=kx+b
�ѣ�-3��0������0��3�������
$\left\{\begin{array}{l}{-3k+b=0}\\{b=3}\end{array}\right.$
��ã�$\left\{\begin{array}{l}{k=1}\\{b=3}\end{array}\right.$��
�����ʽΪy�Tx+3
��x=-2ʱ��y=1
��P��-2��1����
�֡�D��-2��-1����
��PD=2��
t=2��
�൱��PAC�ܳ���Сʱ��t=2��
����ͼ2��
��PA=ACʱ��P�����������3��P�ڶԳ����ϣ�P��-2��3����
D��-2��-1����PD=3-��-1��=4��t=PD=4��
��PC=ACʱ����P��-2��b������
4+��b-3��2=1+9�����b=3+$\sqrt{6}$��b=3-$\sqrt{6}$��
��P�壨-2��3+$\sqrt{6}$����PD=3+$\sqrt{6}$-��-1��=4+$\sqrt{6}$��t=PD=4+$\sqrt{6}$��
P�䣨-2��3-$\sqrt{6}$����PD=3-$\sqrt{6}$-��-1��=4-$\sqrt{6}$��t=PD=4-$\sqrt{6}$��
�ʴ�Ϊ��2��4+$\sqrt{6}$��4-$\sqrt{6}$��
�۴��ڵ�P
����C��CM�ͶԳ��ᣬ����ΪM���Գ�����X�ύ�ڵ�N����ͼ3�� ��
��
��P��-2��m����
��PN=m AN=1 MC=2 MP=3-m
�ߡ�CMP=��ANP=90��
�֡ߡ�APC=90��
���MPC+��APN=90��
�֡�Rt��MPC��
��MPC+��MCP=90��
���APN=��MCP
���MPC�ס�NAP
��$\frac{CM}{MP}$=$\frac{PN}{AN}$
��$\frac{2}{3-m}$=$\frac{m}{1}$
��m2-3m+2=0
��m1=1 m2=2
��P��-2��1������-2��2����
���� ���⿼���˶��κ����ۺ��⣬���ô���ϵ������������ʽ�������߶δ�ֱƽ�����ϵĵ㵽�߶����˵�ľ�����ȣ�����֮���߶���̵ó�P�������ǽ���ؼ������ݵ��������εĶ���ó�P�������ǽ���ؼ���Ҫ�������ۣ��Է���©���������������ε��ж������ʵó�m�ķ����ǽ���ؼ���Ҫ�������ۣ��Է���©��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
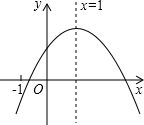 ���κ���ͼ����ͼ��ʾ���Գ���Ϊx=1���������н��ۣ�
���κ���ͼ����ͼ��ʾ���Գ���Ϊx=1���������н��ۣ�| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
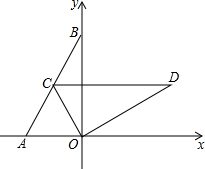 ��֪��ͼ����ֱ������ϵxOy�У���A����B����ֱ�Ϊ��-1��0������0��$\sqrt{3}$��������AB��OD�ɡ�AOB��O��˳ʱ����ת60����ã�
��֪��ͼ����ֱ������ϵxOy�У���A����B����ֱ�Ϊ��-1��0������0��$\sqrt{3}$��������AB��OD�ɡ�AOB��O��˳ʱ����ת60����ã��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
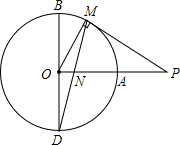 ��ͼ��BD�ǡ�O��ֱ����OA��OB����M���ӻ�AB��һ���㣨�����A��B�غϣ�������M����O������MP��OA���ӳ����ڵ�P��MD��OA���ڵ�N��
��ͼ��BD�ǡ�O��ֱ����OA��OB����M���ӻ�AB��һ���㣨�����A��B�غϣ�������M����O������MP��OA���ӳ����ڵ�P��MD��OA���ڵ�N���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com