

���� ��1�����ݴ���ϵ�����ɵú�������ʽ�������Ա����뺯��ֵ�Ķ�Ӧ��ϵ���ɵ�B�����꣬���ݹ��ɶ������涨�����ɵô𰸣�
��2���������������ε����ʣ��ɵ�$\frac{AM}{MN}$=$\frac{BO}{OA}$=$\frac{1}{2}$������BN��AN�Ĺ�ϵ���ɵ�n���ɵô𰸣�
��3���������������ε��ж������ʣ������������ɵã�$\frac{MD}{AO}$=$\frac{BN}{BC}$���ɵ�MD����������ĺͲ�ɵ�n��ֵ���ɵô𰸣�
��� �⣺��1����ͼ����y�ύ�ڵ�A��0��4����
��m=4���ѵ�C��������뺯������ʽ����a=-$\frac{1}{4}$��
���κ�������ʽΪy=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4��
��y=0ʱ��-$\frac{1}{4}$x2+$\frac{3}{2}$x+4=0�����x=8��x=-2��
���B��������-2��0����
��AB2=BO2+AO2=20��AC2=AO2+OC2=80��
��BC2=��BO+OC��2=100��
�ڡ�ABC�У�AB2+AC2=BC2��
���ABC��ֱ�������Σ�
��2�����N��������n��0������BN=n+2��
�ߡ�AOB=��NMA=90�㣬
�������������
�ٵ�$\frac{AM}{MN}$=$\frac{BO}{OA}$=$\frac{1}{2}$ʱ���á�BAO=��ANM=��BNM��
��NB=NA��
��BN2=NA2��
����n+2��2=n2+42�����n=3����ʱN��3��0����
�ڵ�$\frac{AM}{MN}$=$\frac{OA}{BO}$=2ʱ��d��N��ԭ��O�غϣ�
���ʱN��0��0����
��3�����N��������n��0����-2��n��8����BN=n+2��
��M����MD��x���ڵ�D��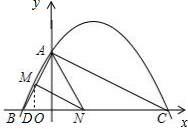 ��
��
��MD��OA�����BMD�ס�BAO��
��$\frac{BM}{BA}$=$\frac{MD}{AO}$��
��MN��AC��$\frac{BM}{BA}$=$\frac{BN}{BC}$��
��$\frac{MD}{AO}$=$\frac{BN}{BC}$��
��OA=4��BC=10��BN=n+2��
��MD=$\frac{2}{5}$��n+2����
��S��AMN=S��ABN-S��BMN=-$\frac{1}{5}$��n-3��2+5=3��
���n=3$��\sqrt{10}$��
��N��������3+$\sqrt{10}$��0����3-$\sqrt{10}$��0����
���� ���⿼���˶��κ����ۺ��⣬���ô���ϵ������������ʽ�����ù��ɶ������涨���ǽ���ؼ����������������ε����ʵó�BN��AN�Ĺ�ϵ�ǽ���ؼ����������������ε��ж������ʵó�MD��ֵ�ǽ���ؼ���������������ĺͲ�ó�N��ֵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪������y=ax2+bx+c��x�����������A��B����ֱ�Ϊ��-1��0������-3��0������������y�ύ��CΪ��0��3����
��ͼ����֪������y=ax2+bx+c��x�����������A��B����ֱ�Ϊ��-1��0������-3��0������������y�ύ��CΪ��0��3�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | k��0 | B�� | k��-1 | C�� | k��-2 | D�� | k��-3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
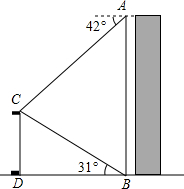 ��ͼ��ijУ��ѧ��ȤС����¥AB�Ķ���A����ø�¥��ǰ�����CD�Ķ���C�ĸ���Ϊ42�㣬��¥AB�ĵײ�B��������CD�Ķ���C������Ϊ31�㣬��֪���CD�ĸ߶�Ϊ12m�����ݲ�õ����ݣ�����¥AB�ĸ߶ȣ����������������
��ͼ��ijУ��ѧ��ȤС����¥AB�Ķ���A����ø�¥��ǰ�����CD�Ķ���C�ĸ���Ϊ42�㣬��¥AB�ĵײ�B��������CD�Ķ���C������Ϊ31�㣬��֪���CD�ĸ߶�Ϊ12m�����ݲ�õ����ݣ�����¥AB�ĸ߶ȣ�����������������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
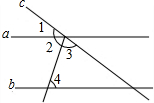 ��ͼ��ֱ��a��b��ֱ��c���أ�a��b������2=��3����4=63�㣬���1���ڣ�������
��ͼ��ֱ��a��b��ֱ��c���أ�a��b������2=��3����4=63�㣬���1���ڣ�������| A�� | 54�� | B�� | 58�� | C�� | 63�� | D�� | 68�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com