
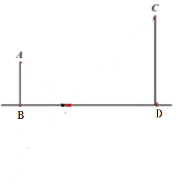
【题目】如图,海上救援船要从距离海岸8海里的![]() 点位置到海岸
点位置到海岸![]() 的
的![]() 处携带救援设备,然后到距离海岸16海里处的
处携带救援设备,然后到距离海岸16海里处的![]() 点处对故障船实施救援.已知
点处对故障船实施救援.已知![]() 间的距离为18海里,为使救援船尽快赶到故障船实施救援,救援设备被放置在恰当位置.
间的距离为18海里,为使救援船尽快赶到故障船实施救援,救援设备被放置在恰当位置.
(1)试在图中确定点![]() 的位置;
的位置;
(2)若救援船的速度是20节(1节=1海里/小时),求这艘救援船最快多长时间到达故障船?
【答案】(1)见解析;(2)1.5
【解析】
(1)利用“直线同侧两点到直线上一点距离的和最短的问题”模型,利用轴对称的知识,确定M的位置.
(2)补全图形,利用勾股定理,得到EC的长,从而得到到达所用时间.
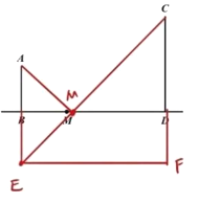
解:(1)延长AB至E,使BE=AB,连接EC交BD于M,连接AM,则点M即为所求.
(2)依题意有AB=8,CD=16,BD=18,
根据(1)的作图可知,点A,E关于直线BD对称,
∴AB=BE=8,AM=EM,
过点E作EF![]() BD,交CD的延长线与F,
BD,交CD的延长线与F,
∵四边形BEFD为矩形,
∴EF=BD=18,AB=BE=DF=8,
∴CF=CD+DF=16+8=24,
在![]() ECF中,
ECF中,![]() ,
,
∴AM+MC=EM+MC=EC=30,
又∵救援船的速度是20节,即为20×1=20(海里/小时),
∵![]() (小时).
(小时).
∴这艘救援船最快到达故障船的时间为1.5小时.


科目:初中数学 来源: 题型:
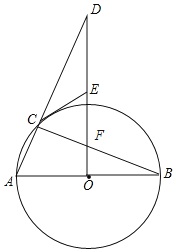
【题目】如图,AB是⊙O的直径,DO⊥AB于点O,连接DA交⊙O于点C,过点C作⊙O的切线交DO于点E,连接BC交DO于点F.
(1)求证:CE=EF;
(2)连接AF并延长,交⊙O于点G.填空:
①当∠D的度数为 时,四边形ECFG为菱形;
②当∠D的度数为 时,四边形ECOG为正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=(x+2)2+m的图象与y轴交于点C,点B在抛物线上,且与点C关于抛物线的对称轴对称,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(﹣1,0)及点B.
(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足(x+2)2+m≥kx+b的x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1,图2是两张形状、大小完全相同的6×6方格纸,方格纸中的每个小长方形的边长为1,所求的图形各顶点也在格点上.

(1)在图1中画一个以点![]() ,
,![]() 为顶点的菱形(不是正方形),并求菱形周长;
为顶点的菱形(不是正方形),并求菱形周长;
(2)在图2中画一个以点![]() 为所画的平行四边形对角线交点,且面积为6,求此平行四边形周长.
为所画的平行四边形对角线交点,且面积为6,求此平行四边形周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=![]() 的图象相交于点A(m,3)、B(﹣6,n),与x轴交于点C.
的图象相交于点A(m,3)、B(﹣6,n),与x轴交于点C.
(1)求一次函数y=kx+b的关系式;
(2)结合图象,直接写出满足kx+b>![]()
![]() 的x的取值范围;
的x的取值范围;
(3)若点P在x轴上,且S△ACP=![]() S△BOC,求点P的坐标.
S△BOC,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是( )

A. 55° B. 60° C. 65° D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】莲城超市以10元/件的价格调进一批商品,根据前期销售情况,每天销售量y(件)与该商品定价x(元)是一次函数关系,如图所示.
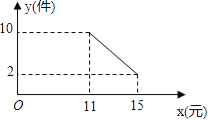
(1)求销售量y与定价x之间的函数关系式;
(2)如果超市将该商品的销售价定为13元/件,不考虑其它因素,求超市每天销售这种商品所获得的利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点
中,点![]() 是
是![]() 边上一个动点,过点
边上一个动点,过点![]() 作直线
作直线![]() ,设
,设![]() 交
交![]() 的平分线于点
的平分线于点![]() ,交
,交![]() 的外角平分线于点
的外角平分线于点![]() .
.
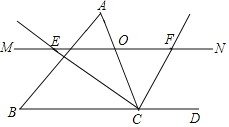
(1)探究![]() 与
与![]() 的数量关系并加以证明;
的数量关系并加以证明;
(2)当点![]() 运动到
运动到![]() 上的什么位置时,四边形
上的什么位置时,四边形![]() 是矩形,请说明理由;
是矩形,请说明理由;
(3)在(2)的基础上,![]() 满足什么条件时,四边形
满足什么条件时,四边形![]() 是正方形?为什么?
是正方形?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com