
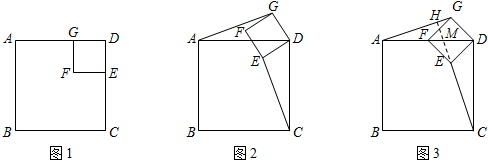
分析 (1)利用SAS证△ADG≌△CDE即可;
(2)①同样先证明△ADG≌△CDE,得出∠DAG=∠DCE,而∠DCM+∠DMC=90°,从而∠DAG+∠AMH=90°,结论显然;
②连接AC、CG,注意到DG∥AC,△GAC与△DAC的面积相等,于是考虑用等积变换,求出AG即可求出CH;
(3)A、C、G三点固定,将△ACG每边作为平行四边形的对角线就得出三种情况,画出相应的图形,相应的CN长可直接算出;
解答 解:(1)成立.如图2,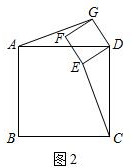
∵∠CDE+∠EDA=∠ADG+∠ADE=90°,
∴∠ADG=∠CDE,
在△ADG和△CDE中,
$\left\{\begin{array}{l}{DG=DE}\\{∠ADG=∠CDE}\\{AD=CD}\end{array}\right.$,
∴△ADG≌△CDE(SAS),
∴AG=CE;
(2)如图3,过点E作EP⊥CD于点P,连接AC,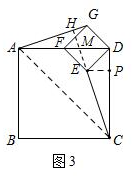
①同(1)可证△ADG≌△CDE,
∴∠DAG=∠DCE,
∵∠DCM+∠DMC=90°,
∴∠DAG+∠AMH=90°,
∴AG⊥CH;
②∵∠EDF=∠EDC=45°,DG=$\sqrt{2}$,
∴DP=EP=1,
∵CD=AD=4,
∴CP=3,
∴CE=$\sqrt{10}$,
∴AG=$\sqrt{10}$,
∵∠DAC=∠ADG=45°,
∴DG∥AC,
∴S△AGC=S△ADC=$\frac{1}{2}×4×4$=8,
∵${S}_{△AGC}=\frac{1}{2}×AG×CH$,
∴$CH=\frac{16}{\sqrt{10}}=\frac{8\sqrt{10}}{5}$;
(3)①如图4,NADG是平行四边形,
此时,CN=CA+AN=CA+DG=$4\sqrt{2}+\sqrt{2}$=$5\sqrt{2}$;
②如图5,ANDG是平行四边形,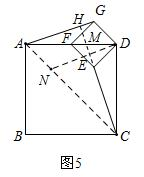
此时,CN=CA-AN=CA-DG=$4\sqrt{2}-\sqrt{2}$=$3\sqrt{2}$;
③如图6,GADN是平行四边形,延长CD交GN于点R,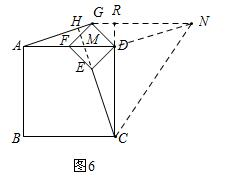
则CR=CD+RD=4+1=5,
RN=GN-GR=4-1=3,
∴CN=$\sqrt{C{R}^{2}+R{N}^{2}}$=$\sqrt{34}$.
点评 本题考查了正方形的性质、全等三角形的判定与性质、三角形内角和性质、等积变换、勾股定理、平行四边形的判定与性质等知识点,难度较大.第(2)小题证明AG⊥CH体现全等三角形的重要性质,即两个全等三角形只要有一组对边是相互垂直的,那么剩下两组对应边也是相互垂直的,在一些大型的题目中可直接使用这个性质;本题求CH的长度使用了等积变换方法,大大减少了运算量,如果不用等积变换而采用相似等其它手段则运算要复杂得多;至于第(3)小题找平行四边形的关键是知道有三个点是固定的,那么只需要将这三个点所形成的三角形的三边分别作为平行四边形对角线即可迅速画出三种情况,并且求CN的长也是很容易的.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
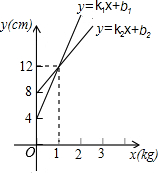 若甲、乙两弹簧的长度ycm与所挂物体质量xkg之间的函数表达式分别为y=k1x+b1和y=k2x+b2,如图所示,所挂物体质量均为2kg时,甲弹簧长为y1,乙弹簧长为y2,则y1与y2的大小关系为( )
若甲、乙两弹簧的长度ycm与所挂物体质量xkg之间的函数表达式分别为y=k1x+b1和y=k2x+b2,如图所示,所挂物体质量均为2kg时,甲弹簧长为y1,乙弹簧长为y2,则y1与y2的大小关系为( )| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不能确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com