
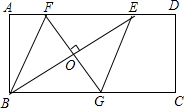
 如图,矩形ABCD中,AD=2AB,E是AD边上一点,DE=
如图,矩形ABCD中,AD=2AB,E是AD边上一点,DE=| 1 |
| n |
| S1 |
| S2 |
| 17 |
| 30 |
|
|
| 4 |
| 3 |
| 5 |
| 3 |
| 7 |
| 24 |
| 25 |
| 24 |
| 1 |
| 2 |
| 5 |
| 4 |
| 2x |
| n |
| S1 |
| S2 |
| 17 |
| 30 |
| BG•AB |
| AB•AD |
| 17 |
| 30 |
| 17 |
| 15 |
| 8 |
| 15 |
| 5 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2x |
| n |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图1,在一个不透明的袋中装有四个球,分别标有字母A、B、C、D,这些球除了所标字母外都相同,另外,有一面白色、另一面黑色、大小相同的4张正方形卡片,每张卡片上面的字母相同,分别标有A、B、C、D.最初,摆成图2的样子,A、D是黑色,B、C是白色.
如图1,在一个不透明的袋中装有四个球,分别标有字母A、B、C、D,这些球除了所标字母外都相同,另外,有一面白色、另一面黑色、大小相同的4张正方形卡片,每张卡片上面的字母相同,分别标有A、B、C、D.最初,摆成图2的样子,A、D是黑色,B、C是白色.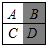 )
)查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知AB是⊙O的直径,BP是⊙O的弦,弦CD⊥AB于点F,交BP于点G,E在CD的延长线上,EP=EG,
如图,已知AB是⊙O的直径,BP是⊙O的弦,弦CD⊥AB于点F,交BP于点G,E在CD的延长线上,EP=EG,
| ||
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
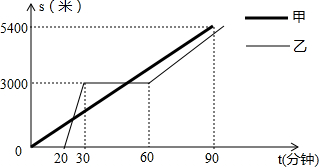 某景区的三个景点A、B、C在同一线路上,甲、乙两名游客从景点A出发,甲步行到景点C,乙乘景区观光车先到景点B,在B处停留一段时间后,再步行到景点C.甲、乙两人离开景点A后的路程S(米)关于时间t(分钟)的函数图象如图所示.根据以上信息回答下列问题:
某景区的三个景点A、B、C在同一线路上,甲、乙两名游客从景点A出发,甲步行到景点C,乙乘景区观光车先到景点B,在B处停留一段时间后,再步行到景点C.甲、乙两人离开景点A后的路程S(米)关于时间t(分钟)的函数图象如图所示.根据以上信息回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
 某校课外兴趣小组在本校学生中开展“感动中国2013年度人物”先进事迹知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A、B、C、D四类.其中,A类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”,D类表示“不太了解”,划分类别后的数据整理如下表:
某校课外兴趣小组在本校学生中开展“感动中国2013年度人物”先进事迹知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A、B、C、D四类.其中,A类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”,D类表示“不太了解”,划分类别后的数据整理如下表:| 类别 | A | B | C | D |
| 频数 | 30 | 40 | 24 | b |
| 频率 | a | 0.4 | 0.24 | 0.06 |
查看答案和解析>>
科目:初中数学 来源: 题型:
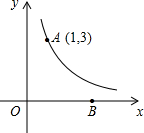 如图,反比例函数y=
如图,反比例函数y=| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
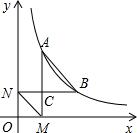 如图,已知反比例函数y=
如图,已知反比例函数y=| k |
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com