
【题目】定义:在平面内,我们把既有大小又有方向的量叫做平面向量。平面向量可以用有向线段表示,有向线段的长度表示向量的大小,有向线段的方向表示向量的方向。其中大小相等,方向相同的向量叫做相等向量。如以正方形![]() 的四个顶点中某一点为起点,另一个顶点为终点作向量,可以作出8个不同的向量:
的四个顶点中某一点为起点,另一个顶点为终点作向量,可以作出8个不同的向量:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() (由于
(由于![]() 和
和![]() 是相等向量,因此只算一个)
是相等向量,因此只算一个)
⑴作两个相邻的正方形(如图一)。以其中的一个顶点为起点,另一个顶点为终点作向量,可以作出不同向量的个数记为![]() ,试求
,试求![]() 的值;
的值;
⑵作![]() 个相邻的正方形(如图二)“一字型”排开。以其中的一个顶点为起点,另一个顶点为终点作向量,可以作出不同向量的个数记为
个相邻的正方形(如图二)“一字型”排开。以其中的一个顶点为起点,另一个顶点为终点作向量,可以作出不同向量的个数记为![]() ,试求
,试求![]() 的值;
的值;
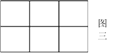
⑶作![]() 个相邻的正方形(如图三)排开。以其中的一个顶点为起点,另一个顶点为终点作向量,可以作出不同向量的个数记为
个相邻的正方形(如图三)排开。以其中的一个顶点为起点,另一个顶点为终点作向量,可以作出不同向量的个数记为![]() ,试求
,试求![]() 的值;
的值;
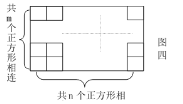
⑷作![]() 个相邻的正方形(如图四)排开。以其中的一个顶点为起点,另一个顶点为终点作向量,可以作出不同向量的个数记为
个相邻的正方形(如图四)排开。以其中的一个顶点为起点,另一个顶点为终点作向量,可以作出不同向量的个数记为![]() ,试求
,试求![]() 的值。
的值。
![]()

【答案】⑴ ![]() ;⑵
;⑵ ![]() ;⑶
;⑶![]() ;⑷
;⑷![]() .
.
【解析】
(1)根据图形,即可求得f(2)的值;
(2)首先求f(1),f(2),f(3),f(4),所以得到规律为:f(n)=6n+2;
(3)根据图形,即可求得f(2×3)的值;
(4)先分析特殊情况,再求得规律:f(m×n)=2(m+n)+4mn.
(1)作两个相邻的正方形,以其中的一个顶点为起点,另一个顶点为终点作向量,可以作出不同向量的个数f(2)=14;
(2)分别求出作两个、三个、四个相邻的正方形(如图1).以其中的一个顶点为起点,另一个顶点为终点作向量,可以作出不同的向量个数,找出规律,
∵f(1)=6×1+2=8,f(2)=6×2+2=14,f(3)=6×3+2=20,f(4)=6×4+2=26,
∴f(n)=6n+2;
(3)f(2×3)=34;
(4)∵f(2×2)=24,f(2×3)=34,f(2×4)=44,f(3×2)=34,f(3×3)=48,f(3×4)=62
∴f(m×n)=2(m+n)+4mn.


 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】如图已知:![]() 是圆
是圆![]() 的直径,
的直径,![]() ,点
,点![]() 为圆
为圆![]() 上异于点
上异于点![]() 、
、![]() 的一点,点
的一点,点![]() 为弦
为弦![]() 的中点.
的中点.
(1)如果![]() 交
交![]() 于点
于点![]() ,求
,求![]() :
:![]() 的值;
的值;
(2)如果![]() 于点
于点![]() ,求
,求![]() 的正弦值;
的正弦值;
(3)如果![]() ,
,![]() 为
为![]() 上一动点,过
上一动点,过![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,与射线
,与射线![]() 交于圆内点
交于圆内点![]() ,请完成下列探究.
,请完成下列探究.
探究一:设![]() ,
,![]() ,求
,求![]() 关于
关于![]() 的函数解析式及其定义域.
的函数解析式及其定义域.
探究二:如果点![]() 在以
在以![]() 为圆心,
为圆心,![]() 为半径的圆上,写出此时
为半径的圆上,写出此时![]() 的长度.
的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
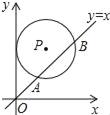
【题目】如图,在平面直角坐标系中,⊙P的圆心是(3,a)(a>3),⊙P与y轴相切,函数y=x的图象被⊙P截得的弦AB的长为2![]() ,则a的值是_____.
,则a的值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
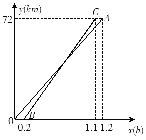
【题目】甲、乙两人周末从同一地点出发去某景点,因乙临时有事,甲先出发,甲出发0.2小时后乙开汽车前往,设甲行驶的时间为x(h),甲、乙两人行驶的路程分别为y1(km)与y2(km),如图是y1与y2关于x的函数图像.
(1)求x为何值时,两人相遇?
(2)求x为何值时,两人相距5km?(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(8,0),O为坐标原点,P是线段OA上任意一点(不含端点O、A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D.当OD=AD=5时,这两个二次函数的最大值之和等于_______
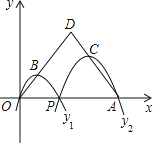
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学家的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.如图这个三角形的构造法其两腰上的数都是1,其余每个数均为其上方左右两数之和,它给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.利用 规律计算:25-5×24+10×23-10×22+5×2-1的值为____.
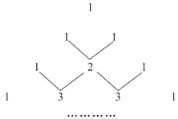
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位射击运动员参加射击训练,各射击20次,成绩如下表所示:
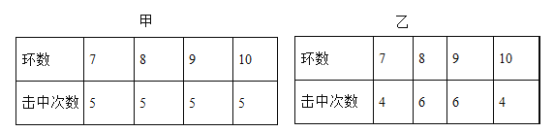
设甲、乙两位运动员射击成绩的方差分别为S 2甲和S 2乙,则下列说法正确的是
A. S 2甲<S 2乙B. S 2甲=S 2乙
C. S 2甲>S 2乙D. 无法比较S 2甲和S 2乙的大小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点 A,B,C,D 依次在同一条直线上,点 E,F 分别在直线 AD 的两侧,已知 BE//CF,∠A=∠D,AE=DF.
(1)求证:四边形 BFCE 是平行四边形.
(2)若 AD=10,EC=3,∠EBD=60°,当四边形 BFCE是菱形时,求 AB 的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加强中小学生安全教育,某校九(1)班组织了“防溺水”知识竞赛,班委会决定购买钢笔和圆珠笔对表现优异的同学进行奖励,同学们前往商店采购,商店里的阿姨说:“购买3支钢笔和2支圆珠笔共需8元,并且3支钢笔比2支圆珠笔多花4元”
(1)求钢笔和圆珠笔每支各需多少元?
(2)班委会决定购买钢笔和圆珠笔共30支,且支出不超过50元,则最多能够购买多少支钢笔?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com