
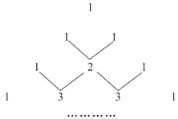
【题目】我国古代数学家的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.如图这个三角形的构造法其两腰上的数都是1,其余每个数均为其上方左右两数之和,它给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.利用 规律计算:25-5×24+10×23-10×22+5×2-1的值为____.
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5)。
的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5)。
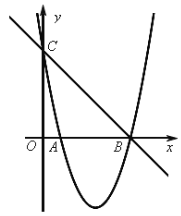
(1)求直线BC与抛物线的解析式;
(2)若点M是抛物线在x轴下方图象上的动点,过点M作MN∥y轴交直线BC于点N,求MN的最大值;
(3)在(2)的条件下,MN取得最大值时,若点P是抛物线在x轴下方图象上任意一点,以BC为边作平行四边形CBPQ,设平行四边形CBPQ的面积为S1,△ABN的面积为S2,且S1=6S2,求点P的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
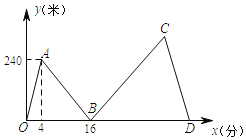
【题目】甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人间的距离y(米)与甲出发的时间x(分)之间的关系如图中折线OA-AB-BC-CD所示.
(1)求线段AB的表达式,并写出自变量x的取值范围;
(2)求乙的步行速度;
(3)求乙比甲早几分钟到达终点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面内,我们把既有大小又有方向的量叫做平面向量。平面向量可以用有向线段表示,有向线段的长度表示向量的大小,有向线段的方向表示向量的方向。其中大小相等,方向相同的向量叫做相等向量。如以正方形![]() 的四个顶点中某一点为起点,另一个顶点为终点作向量,可以作出8个不同的向量:
的四个顶点中某一点为起点,另一个顶点为终点作向量,可以作出8个不同的向量:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() (由于
(由于![]() 和
和![]() 是相等向量,因此只算一个)
是相等向量,因此只算一个)
⑴作两个相邻的正方形(如图一)。以其中的一个顶点为起点,另一个顶点为终点作向量,可以作出不同向量的个数记为![]() ,试求
,试求![]() 的值;
的值;
⑵作![]() 个相邻的正方形(如图二)“一字型”排开。以其中的一个顶点为起点,另一个顶点为终点作向量,可以作出不同向量的个数记为
个相邻的正方形(如图二)“一字型”排开。以其中的一个顶点为起点,另一个顶点为终点作向量,可以作出不同向量的个数记为![]() ,试求
,试求![]() 的值;
的值;
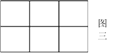
⑶作![]() 个相邻的正方形(如图三)排开。以其中的一个顶点为起点,另一个顶点为终点作向量,可以作出不同向量的个数记为
个相邻的正方形(如图三)排开。以其中的一个顶点为起点,另一个顶点为终点作向量,可以作出不同向量的个数记为![]() ,试求
,试求![]() 的值;
的值;
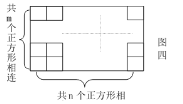
⑷作![]() 个相邻的正方形(如图四)排开。以其中的一个顶点为起点,另一个顶点为终点作向量,可以作出不同向量的个数记为
个相邻的正方形(如图四)排开。以其中的一个顶点为起点,另一个顶点为终点作向量,可以作出不同向量的个数记为![]() ,试求
,试求![]() 的值。
的值。
![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
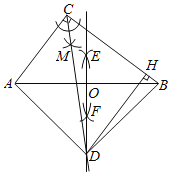
【题目】如图所示,是小聪同学在一次数学兴趣小组活动中,用直尺和圆规对Rt△ACB(∠ACB=90°)进行了如下操作:
①作边AB的垂直平分线EF交AB于点O;
②作∠ACB的平分线CM,CMEF相交于点D;
③连接AD,BD.
请你根据操作,观察图形解答下列问题:
(1)△ABD的形状是______;
(2)若DH⊥BC于点H,已知AC=6,BC=8,求BH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】苏科版九年级下册数学课本91页有这样一道习题:


(1)复习时,小明与小亮、数学老师交流了自己的两个见解,并得到了老师的认可:
①可以假定正方形的边长AB=4a,则AE=DE=2a,DF=a,利用“两边分别成比例且夹角相等的两个三角形相似”可以证明△ABE∽△DEF;请结合提示写出证明过程.
②图中的相似三角形共三对,而且可以借助于△ABE与△DEF中的比例线段来证明△EBF与它们相似.证明过程如下:

(2)交流之后,小亮尝试对问题进行了变化,在老师的帮助下,提出了新的问题,请你解答:
已知:如图,在矩形ABCD中,E为AD的中点,EF⊥EC交AB于F,连结FC.
(AB>AE)

①求证:△AEF∽△ECF;
②设BC=2,AB=a,是否存在a值,使得△AEF与△BFC相似.若存在,请求出a的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,F,且BE=DF.
(1)求证:ABCD是菱形;
(2)若AB=5,AC=6,求ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年9月,我国中小学生迎来了新版“教育部统编义务教育语文教科书”,本次“统编本”教材最引人关注的变化之一是强调对传统文化经典著作的阅读,某校对A《三国演义》、B《红楼梦》、C《西游记》、D《水浒》四大名著开展“最受欢迎的传统文化经典著作”调查,随机调查了若干名学生(每名学生必选且只能选这四大名著中的一部)并将得到的信息绘制了下面两幅不完整的统计图:

(1)本次一共调查了 名学生;
(2)请将条形统计图补充完整;
(3)某班语文老师想从这四大名著中随机选取两部作为学生暑期必读书籍,请用树状图或列表的方法求恰好选中《三国演义》和《红楼梦》的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com