
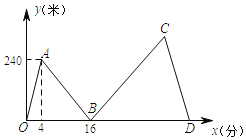
【题目】甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人间的距离y(米)与甲出发的时间x(分)之间的关系如图中折线OA-AB-BC-CD所示.
(1)求线段AB的表达式,并写出自变量x的取值范围;
(2)求乙的步行速度;
(3)求乙比甲早几分钟到达终点?
【答案】(1)![]() ;(2)80米/分;(3)6分钟
;(2)80米/分;(3)6分钟
【解析】
(1)根据图示,设线段AB的表达式为:y=kx+b,把把(4,240),(16,0)代入得到关于k,b的二元一次方程组,解之,即可得到答案,
(2)根据线段OA,求出甲的速度,根据图示可知:乙在点B处追上甲,根据速度=路程÷时间,计算求值即可,
(3)根据图示,求出二者相遇时与出发点的距离,进而求出与终点的距离,结合(2)的结果,分别计算出相遇后,到达终点甲和乙所用的时间,二者的时间差即可所求答案.
(1)根据题意得:
设线段AB的表达式为:y=kx+b (4≤x≤16),
把(4,240),(16,0)代入得:
![]() ,
,
解得:![]() ,
,
即线段AB的表达式为:y= -20x+320 (4≤x≤16),
(2)又线段OA可知:甲的速度为:![]() =60(米/分),
=60(米/分),
乙的步行速度为:![]() =80(米/分),
=80(米/分),
答:乙的步行速度为80米/分,
(3)在B处甲乙相遇时,与出发点的距离为:240+(16-4)×60=960(米),
与终点的距离为:2400-960=1440(米),
相遇后,到达终点甲所用的时间为:![]() =24(分),
=24(分),
相遇后,到达终点乙所用的时间为:![]() =18(分),
=18(分),
24-18=6(分),
答:乙比甲早6分钟到达终点.


科目:初中数学 来源: 题型:
【题目】某学校准备采购一批茶艺耗材和陶艺耗材.经查询,如果按照标价购买两种耗材,当购买茶艺耗材的数量是陶艺耗材数量的2倍时,购买茶艺耗材共需要18000元,购买陶艺耗材共需要12000元,且一套陶艺耗材单价比一套茶艺耗材单价贵150元.
(1)求一套茶艺耗材、一套陶艺耗材的标价分别是多少元?
(2)学校计划购买相同数量的茶艺耗材和陶艺耗材.商家告知,因为周年庆,茶艺耗材的单价在标价的基础上降价2![]() 元,陶艺素材的单价在标价的基础降价150元,该校决定增加采购数量,实际购买茶艺素材和陶艺素材的数量在原计划基础上分别增加了2.5
元,陶艺素材的单价在标价的基础降价150元,该校决定增加采购数量,实际购买茶艺素材和陶艺素材的数量在原计划基础上分别增加了2.5![]() %和
%和![]() ,结果在结算时发现,两种耗材的总价相等,求
,结果在结算时发现,两种耗材的总价相等,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地方卫视有一档冲关游戏,游戏规定:单独一个人参加游戏,以选出正确答案者能顺利过关;两个人一起参加游戏,主要考查两人的默契程度,以两人选出答案的序号一致才能一同顺利过关.
(1)小王单独参加游戏,若选定的问题有5个备选答案,其中有2个答案是正确的,求小王顺利过关的概率;
(2)小王和小李一起参加游戏,若小王的问题有4个备选答案,小李的问题有3个备选答案,求小王和小李能一同顺利过关的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
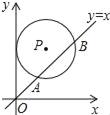
【题目】如图,在平面直角坐标系中,⊙P的圆心是(3,a)(a>3),⊙P与y轴相切,函数y=x的图象被⊙P截得的弦AB的长为2![]() ,则a的值是_____.
,则a的值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】动画片《小猪佩奇》分靡全球,受到孩子们的喜爱.现有4张《小猪佩奇》角色卡片,分别是A佩奇,B乔治,C佩奇妈妈,D佩奇爸爸(四张卡片除字母和内容外,其余完全相同).姐弟两人做游戏,他们将这四张卡片混在一起,背面朝上放好.
(1)姐姐从中随机抽取一张卡片,恰好抽到A佩奇的概率为 ;
(2)若两人分别随机抽取一张卡片(不放回),请用列表或画树状图的分方法求出恰好姐姐抽到A佩奇弟弟抽到B乔治的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
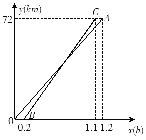
【题目】甲、乙两人周末从同一地点出发去某景点,因乙临时有事,甲先出发,甲出发0.2小时后乙开汽车前往,设甲行驶的时间为x(h),甲、乙两人行驶的路程分别为y1(km)与y2(km),如图是y1与y2关于x的函数图像.
(1)求x为何值时,两人相遇?
(2)求x为何值时,两人相距5km?(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
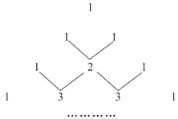
【题目】我国古代数学家的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.如图这个三角形的构造法其两腰上的数都是1,其余每个数均为其上方左右两数之和,它给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.利用 规律计算:25-5×24+10×23-10×22+5×2-1的值为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
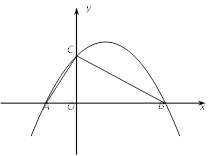
【题目】如图,已知二次函数y=ax2-4ax+c的图像交x轴于A、B两点(其中A点在B点的左侧),交y轴于点C(0,3).
(1)若tan∠ACO=![]() ,求这个二次函数的表达式;
,求这个二次函数的表达式;
(2)若OC为OA、OB的比例中项.
①设这个二次函数的顶点为P,求△PBC的面积;
②若M为y轴上一点,N为平面内一点,问:是否存在这样的M、N,使得以M、N、B、C为顶点的四边形为矩形?若存在,请直接写出所有符合条件的点N的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com