
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�AB��CD��x�ᣬBC��DE��y�ᣬ��AB��CD��4 cm��OA��5 cm��DE��2 cm������P�ӵ�A��������ÿ��1 cm���ٶȣ���ABC·�����C�˶�������Q�ӵ�O��������ÿ��2 cm���ٶȣ���OED·�����D�˶�����P��Q����ͬʱ����������һ�㵽���յ�ʱ���˶�ֹͣ��
(1)ֱ��д��B��C��D����������ꣻ
(2)��P��Q�������3 sʱ����������PQC�������
(3)�������˶���ʱ��Ϊt s���ú�t��ʽ�ӱ�ʾ�˶�������������OPQ�������
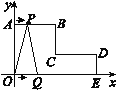
���𰸡���1��B��4��5����C��4��2����D��8��2������2��2����3�� ![]() .
.
��������
��1������ƽ��ֱ������ϵд����������꼴�ɣ�
��2���������P��Q�����꣬�����CP��CQ��Ȼ����������ε������ʽ��ʽ���㼴�ɵý⣻
��3���������P��A�˶���C��ʱ��Ҫ7�룬��Q��O�˶���D��ʱ��Ҫ5�룬��������һ�㵽���յ�ʱ���˶�ֹͣ����֪�˶�ʱ��t��ȡֵ��ΧΪ0��t��5��Ȼ�������������ۼ���.��������ֱ�Ϊ��0��t��4����ʱ��P��AB�ϣ���Q��OE�ϣ���4��t��5����ʱ��P��BC�ϣ���Q��DE��.
(1)��AB��CD��x�ᣬBC��DE��y�ᣬ��AB=CD=4��OA=5��DE=2��
4+4=8��
��B(4��5)��C(4��2)��D(8��2)��
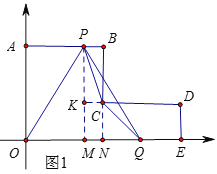
(2)��P��Q�����˶�3 sʱ����ͼ1����ʱ��P(3��5)��Q(6��0)��
��ΪC(4��2)������P��PM��x�ᣬ�ӳ�BC��x���ڵ�N���ӳ�DC��PM�ڵ�K��
����M(3��0)��N��4��0����K��3��2����
����QM��MQ=3��CK=MN=1��PK=BC=3��CN=NQ=2��
����������PQC�������![]() ��3��5��
��3��5��![]() ��1��3��
��1��3��![]() ��2��2��2��1��2��
��2��2��2��1��2��
(3)��P�˶���·����ΪAB+BC=4+3=7����ʱ��Ҫ7�룬
��Q�˶���·����ΪOE+DE=8+2=10����ʱ��Ҫ5�룬
��������һ�㵽���յ�ʱ���˶�ֹͣ����֪�˶�ʱ��t��ȡֵ��ΧΪ0��t��5��
�ٵ�0��t��4ʱ(��ͼ2)��OA��5��OQ��2t��
S������OPQ��![]() OQOA��
OQOA��![]() ��2t��5��5t������
��2t��5��5t������
�ڵ�4��t��5ʱ(��ͼ3)��OE��8��EM��9��t��PM��4��MQ��17��3t��EQ��2t��8��
S������OPQ��S����OPME��S������PMQ��S������OEQ
��![]() ��(4��8)��(9��t)��
��(4��8)��(9��t)��![]() ��4��(17��3t)��
��4��(17��3t)��![]() ��8��(2t��8)
��8��(2t��8)
��52��8t��
���ϣ�![]() .
.


 �̲�ȫ���ִʾ�ƪϵ�д�
�̲�ȫ���ִʾ�ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijС����ԭ��400ƽ���������γ��ظĽ���300ƽ���ij����γ������ҳ��Ϳ�֮��Ϊ3��2.�����ԭ�������γ��ص���դ��Χǽ��������Χ���³��صij�����Χǽ����ô��Щ��դ���Ƿ��ã���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����С���һ��������һ�ζ���������·���ޣ��涨����Ϊ����������Ϊ����С��ij����ؼ�ΪM��ij��������ʱ������¼(��λ��ǧ��)���£�
+12��-5��-9��+10��-4��+15��-9��+3��-6��-3��-7
(1)���չ�ʱ������С��������M�ж�Զ���ڶ�������ࣿ
(2)������ÿǧ����0.2������ӳ������չ�ʱ���������Ͷ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���BAC��90����AB��AC����DΪBC���е㣬ֱ�ǡ�MDN�Ƶ�D��ת��DM��DN�ֱ����AB��AC����E��F���㣬���н��ۣ��١�DEF�ǵ���ֱ�������Σ���AE��CF���ۡ�BDE�ա�ADF����BE��CF��EF��������ȷ�������� ��
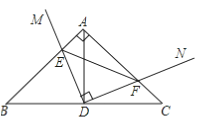
A. �٢ڢ� B. �ڢۢ�
C. �٢ڢ� D. �٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͬһ����·�ϣ��׳���A�ص�B�أ��ҳ���B�ص�A�أ����ȳ�����ͼ�е����߶α�ʾ�ס�������֮��ľ���y��ǧ�ף�����ʻʱ��x(Сʱ)�ĺ�����ϵ��ͼ��.����˵��������ǣ� ��
A.���ȳ�����ʱ��Ϊ0.5Сʱ
B.���ٶ���80ǧ��/Сʱ
C.�׳���0.5Сʱ����������
D.��B�ر��ҵ�A���� ![]() Сʱ
Сʱ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��A(2,3)�͵�B(0,2)����A�ڷ���������y= ![]() ��ͼ����.������AB���ٽ�����AB�Ƶ�A����ʱ�뷽����ת45�㣬������������ͼ���ڵ�C�����C������Ϊ.
��ͼ����.������AB���ٽ�����AB�Ƶ�A����ʱ�뷽����ת45�㣬������������ͼ���ڵ�C�����C������Ϊ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��2018��12�·ݵ�����������ѡ�����еķ��֣���ÿ��������4��λ���ϵ���������ƽ���ͣ�����������磺��32+112������42+102��=14����212+292������222+282��=14�����ѷ��ֽ������14.
(1)������12��12�գ�����дһ���������������ڵ����Ʋ��ֵ���ʽ��
(2)����������ʽ����������Ϲ��ɼ���֤��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У�AB=AC����DΪ����CB��һ�����㣨����B��C�غϣ�����ADΪһ����AD���Ҳ�����ADE��ʹAD=AE����DAE=��BAC������E��EF��BC����ֱ��AC�ڵ�F������CE��
(1)��ͼ�٣�����BAC=60�㣬���߷��ࣺ��CEF�� ____________ �����Σ�
(2)����BAC��60�㣮
����ͼ�ڣ�����D���߶�CB���ƶ�ʱ���жϡ�CEF����״��֤����
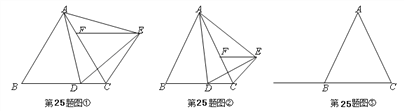
�ڵ���D���߶�CB���ӳ������ƶ�ʱ����CEF��ʲô�����Σ�����ͼ���л�����Ӧ��ͼ�Σ�д�����۲�֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��l1��y=kx��4��ͼ����ֱ��l2��y=![]() x+1��ͼ��ƽ�У�
x+1��ͼ��ƽ�У�
��1����ֱ��l1��ͼ����x�ᣬy����Χ��ͼ�ε������
��2����ԭ�㵽ֱ��l1�ľ��룮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com