练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知直线l1：y=kx﹣4的图象与直线l2：y=x+1的图象平行．

    （1）求直线l1的图象与x轴，y轴所围成图形的面积；

    （2）求原点到直线l1的距离．

    【答案】（1）6；（2）．

    【解析】

    （1）根据平行得出k=，求出与想、y轴的交点坐标，即可求出面积；
    （2）根据垂直求出a的值，求出组成的方程组的解，即可求出答案．

    解：（1）∵直线l1：y=kx﹣4的图象与直线l2：y=x+1的图象平行，

    ∴k=，

    即直线l1：y=x﹣4，

    当x=0时，y=﹣4，

    当y=0时，x=3，

    所以直线l1的图象与x轴，y轴所围成图形的面积是=6；

    （2）设过原点且垂直于直线l1的直线的解析式为y=ax，

    则a=﹣1，

    解得：a=﹣，

    即y=﹣x，

    解方程组 得： ，

    = ，

    即原点到直线l1的距离是 ．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

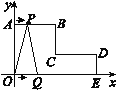
    【题目】如图，在平面直角坐标系中，AB∥CD∥x轴，BC∥DE∥y轴，且AB＝CD＝4 cm，OA＝5 cm，DE＝2 cm，动点P从点A出发，以每秒1 cm的速度，沿ABC路线向点C运动；动点Q从点O出发，以每秒2 cm的速度，沿OED路线向点D运动．若P，Q两点同时出发，其中一点到达终点时，运动停止．

    (1)直接写出B，C，D三个点的坐标；

    (2)当P，Q两点出发3 s时，求三角形PQC的面积；

    (3)设两点运动的时间为t s，用含t的式子表示运动过程中三角形OPQ的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对任意有理数x、y定义运算如下：x△y=ax+by+cxy，这里a、b、c是给定的数，等式右边是通常数的加法及乘法运算，如当a=1，b=2，c=3时，l△3=1×l+2×3+3×1×3=16，现已知所定义的新运算满足条件，1△2=3，2△3=4，并且有一个不为零的数d使得对任意有理数x△d=x，求a、b、c、d的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形ABCD的边长为10，AG=CH=8，BG=DH=6，连接GH，则线段GH的长为（ ）
    A.
    B.2
    C.
    D.10﹣5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在等边△ABC中，AB=4，点P是BC边上的动点，点P关于直线AB，AC的对称点分别为M，N，则线段MN长的取值范围是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①，已知直线y=-2x+4与x轴、y轴分别交于点A、C，以OA、OC为边在第一象限内作长方形OABC．

    （1）求点A、C的坐标；

    （2）将△ABC对折，使得点A的与点C重合，折痕交AB于点D，求直线CD的解析式（图②）；

    （3）在坐标平面内，是否存在点P（除点B外），使得△APC与△ABC全等？若存在，请直接写出所有符合条件的点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点A，B，C在一条直线上，△ABD，△BCE均为等边三角形，连接AE和CD，AE分别交CD，BD于点M，P，CD交BE于点Q，连接PQ，BM，下面结论：

    ①△ABE≌△DBC；②∠DMA=60°；③△BPQ为等边三角形；④MB平分∠AMC，

    其中结论正确的有（ ）

    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，∠C＝90°，AC＝BC，点C在第一象限内．若A(5，0)，B (－2，4)，C(m，n)，则(m＋n)(m－n)的值是__________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某超市计划经销一些特产，经销前，围绕“A：王高虎头鸡，B：羊口咸蟹子，C：桂河芹菜，D：巨淀湖咸鸭蛋”四种特产，在全市范围内随机抽取了部分市民进行问卷调查：“我最喜欢的特产是什么？”（必选且只选一种）．现将调查结果整理后，绘制成如图所示的不完整的扇形统计图和条形统计图．
    （1）请补全扇形统计图和条形统计图；
    （2）若全市有110万市民，估计全市最喜欢“羊口咸蟹子”的市民约有多少万人？
    （3）在一个不透明的口袋中有四个分别写上四种特产标记A、B、C、D的小球（除标记外完全相同），随机摸出一个小球然后放回，混合摇匀后，再随机摸出一个小球，则两次都摸到A的概率是多少？写出分析计算过程．

    查看答案和解析>>

    同步练习册答案