
【题目】如图,正方形ABCD的边长为10,AG=CH=8,BG=DH=6,连接GH,则线段GH的长为( ) 
A.![]()
B.2 ![]()
C.![]()
D.10﹣5 ![]()
【答案】B
【解析】解:如图,延长BG交CH于点E, 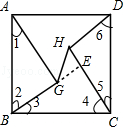
在△ABG和△CDH中,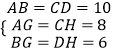 ,
,
∴△ABG≌△CDH(SSS),
AG2+BG2=AB2 ,
∴∠1=∠5,∠2=∠6,∠AGB=∠CHD=90°,
∴∠1+∠2=90°,∠5+∠6=90°,
又∵∠2+∠3=90°,∠4+∠5=90°,
∴∠1=∠3=∠5,∠2=∠4=∠6,
在△ABG和△BCE中,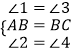 ,
,
∴△ABG≌△BCE(ASA),
∴BE=AG=8,CE=BG=6,∠BEC=∠AGB=90°,
∴GE=BE﹣BG=8﹣6=2,
同理可得HE=2,
在RT△GHE中,GH= ![]() =
= ![]() =2
=2 ![]() ,
,
故选:B.
【考点精析】本题主要考查了勾股定理的概念的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D为BC的中点,直角∠MDN绕点D旋转,DM,DN分别与边AB,AC交于E,F两点,下列结论:①△DEF是等腰直角三角形;②AE=CF;③△BDE≌△ADF;④BE+CF=EF,其中正确结论是( )
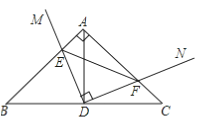
A. ①②④ B. ②③④
C. ①②③ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D为射线CB上一个动点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,过点E作EF∥BC,交直线AC于点F,连接CE.
(1)如图①,若∠BAC=60°,按边分类:△CEF是 ____________ 三角形;
(2)若∠BAC<60°.
①如图②,当点D在线段CB上移动时,判断△CEF的形状并证明;
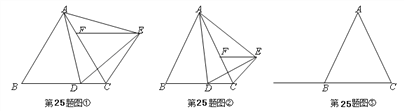
②当点D在线段CB的延长线上移动时,△CEF是什么三角形?请在图③中画出相应的图形,写出结论并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
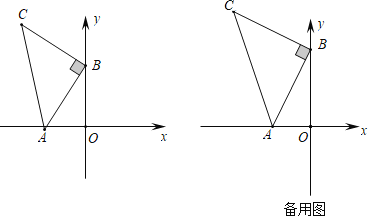
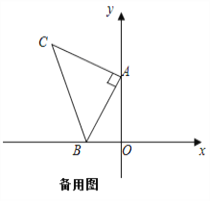
【题目】如图,平面直角坐标系中有点B(﹣1,0)和y轴上一动点A(0,a),其中a>0,以A点为直角顶点在第二象限内作等腰直角△ABC,设点C的坐标为(c,d).
(1)当a=2时,则C点的坐标为( , );
(2)动点A在运动的过程中,试判断c+d的值是否发生变化?若不变,请求出其值;若发生变化,请说明理由.
(3)当a=2时,在坐标平面内是否存在一点P(不与点C重合),使△PAB与△ABC全等?若存在,直接写出P点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)已知甲队每天的施工费用为6500元,乙队每天的施工费用为3500元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乘法公式的探究及应用.
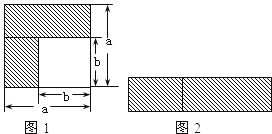
(1)如图1,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是 ,长是 ,面积是 (写成多项式乘法的形式);
(3)比较图1、图2阴影部分的面积,可以得到公式 ;
(4)运用你所得到的公式,计算下列各题:
①10.2×9.8,②(2m+n﹣p)(2m﹣n+p).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l1:y=kx﹣4的图象与直线l2:y=![]() x+1的图象平行.
x+1的图象平行.
(1)求直线l1的图象与x轴,y轴所围成图形的面积;
(2)求原点到直线l1的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
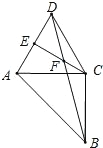
【题目】.如图,以等腰直角△ABC 的直角边 AC 作等边△ACD,CE⊥AD 于 E, BD、CE 交于点 F.
(1)求∠DFE 的度数;
(2)求证:AB=2DF.
查看答案和解析>>
科目:初中数学 来源: 题型:
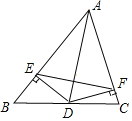
【题目】课本例题
已知:如图,AD是![]() 的角平分线,
的角平分线,![]() ,
,![]() ,垂足分别为E、F.求证:AD垂直平分EF.
,垂足分别为E、F.求证:AD垂直平分EF.
小明做法
证明:因为AD是![]() 的角平分线,
的角平分线,![]() ,
,![]() ,所以
,所以![]()
理由是:“角平分线上的点到这个角的两边的距离相等”.
因为![]() ,
,
所以AD垂直平分EF.
理由是:“到线段两个端点距离相等的点在这条线段的垂直平分线上”.
老师观点
老师说:小明的做法是错误的![]()
请你解决
![]() 指出小明做法的错误;
指出小明做法的错误;
![]() 正确、完整的解决这道题.
正确、完整的解决这道题.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com