
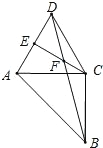
【题目】.如图,以等腰直角△ABC 的直角边 AC 作等边△ACD,CE⊥AD 于 E, BD、CE 交于点 F.
(1)求∠DFE 的度数;
(2)求证:AB=2DF.
【答案】(1)45°;(2)见解析.
【解析】
(1)根据等边三角形的性质可得∠ACD 的大小,根据 BC=CD 即可求得∠CDB,即可求得∠ADB,即可解题;
(2)根据∠DFE=45°可得△DEF 为等腰直角三角形,根据 AD=2DE 即可解题.
(1)∵△ACD 是等边三角形,
∴∠ACD=60°,
∴∠BCD=60°+90°=150°,
∵BC=CD
∴∠BDC= ![]() (180°﹣150°)=15°,
(180°﹣150°)=15°,
∴∠ADF=60°﹣15°=45°,
∴∠DFE=180°﹣∠DEF﹣∠EDF=45°,
(2)∵CE⊥AD,∠DFE= 45°,
∴△DEF 为等腰直角三角形,
∵△ABC 是等腰直角三角形,
∴△ACB∽△DEF,
∴![]() =
=![]() =
=![]() ,
,
∴AB=2DE.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】在面积都相等的所有矩形中,当其中一个矩形的一边长为1时,它的另一边长为3.
(1)设矩形的相邻两边长分别为x,y.
①求y关于x的函数表达式;
②当y≥3时,求x的取值范围;
(2)圆圆说其中有一个矩形的周长为6,方方说有一个矩形的周长为10,你认为圆圆和方方的说法对吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知直线y=-2x+4与x轴、y轴分别交于点A、C,以OA、OC为边在第一象限内作长方形OABC.

(1)求点A、C的坐标;
(2)将△ABC对折,使得点A的与点C重合,折痕交AB于点D,求直线CD的解析式(图②);
(3)在坐标平面内,是否存在点P(除点B外),使得△APC与△ABC全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM,下面结论:
①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形;④MB平分∠AMC,
其中结论正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校数学课题学习小组在“测量教学楼高度”的活动中,设计了以下两种方案:
课题 | 测量教学楼高度 | |
方案 | 一 | 二 |
图示 |
|
|
测得数据 | CD=6.9m,∠ACG=22°,∠BCG=13°, | EF=10m,∠AEB=32°,∠AFB=43° |
参考数据 | sin22°≈0.37,cos22°≈0.93, | sin32°≈0.53,cos32°≈0.85,tan32°≈0.62 |
请你选择其中的一种方法,求教学楼的高度(结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠C=90°,AC=BC,点C在第一象限内.若A(5,0),B (-2,4),C(m,n),则(m+n)(m-n)的值是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B的坐标分别为(1,4)和(4,4),抛物线y=a(x﹣m)2+n的顶点在线段AB上运动(抛物线随顶点一起平移),与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为﹣3,则点D的横坐标最大值为( )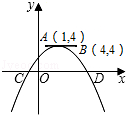
A.﹣3
B.1
C.5
D.8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com