
【题目】如图,正方形A1B1C1O、A2B2C2C1……按照如图所示的方式放置,点A1、A2、A3、…和点C1、C2、C3、…分别在直线y=kx+b(k>0)和x轴上,已知B1(1,1),B2(3,2),B3(7,4),则B2019的坐标是_____.

【答案】(22019﹣1,22018)
【解析】
根据矩形的性质求出点A1、A2的坐标,然后利用待定系数法求一次函数解析式求出k、b,从而得到一次函数解析式,再根据一次函数图象上点的坐标特征求出A4的坐标,然后求出B4的坐标,…,最后根据点的坐标特征的变化规律写出Bn的坐标即可.
解:∵点B1、B2的坐标分别为(1,1),(3,2),
∴A1(0,1),A2(1,2),
∵点A1,A2在直线y=kx+b上,
∴![]() ,
,
解得![]() ,
,
∴y=x+1,
∵点B2的坐标为(3,2),
∴点A3的坐标为(3,4),
∴点B3的坐标为(7,4),
∴点A4的坐标为(7,8),
∴点B4坐标为(15,8),
…,
∴Bn的横坐标是:2n﹣1,纵坐标是:2n﹣1.
∴Bn的坐标是(2n﹣1,2n﹣1),
∴B2019的坐标是(22019﹣1,22018).
故答案为(22019﹣1,22018).


科目:初中数学 来源: 题型:
【题目】(阅读理解)
截长补短法,是初中数学儿何题中一种输助线的添加方法,截长就是在长边上载取一条线段与某一短边相等,补短是通过在一条短边上延长一条线段与另一短边相等,从而解决问题.
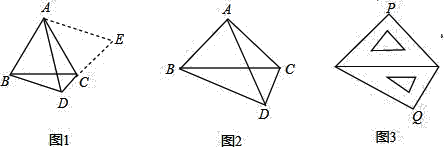
(1)如图1,△ABC是等边三角形,点D是边BC下方一点,∠BDC=120°,探索线段DA、DB、DC之间的数量关系.
解题思路:延长DC到点E,使CE=BD.连接AE,根据∠BAC+∠BDC=180°,可证∠ABD=∠ACE,易证得△ABD≌△ACE,得出△ADE是等边三角形,所以AD=DE,从而探寻线段DA、DB、DC之间的数量关系.
根据上述解题思路,请直接写出DA、DB、DC之间的数量关系是___________
(拓展延伸)
(2)如图2,在Rt△ABC中,∠BAC=90°,AB=AC.若点D是边BC下方一点,∠BDC=90°,探索线段DA、DB、DC之间的数量关系,并说明理由;
(知识应用)
(3)如图3,一副三角尺斜边长都为14cm,把斜边重叠摆放在一起,则两块三角尺的直角项点之间的距离PQ的长为________cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位同学玩摸球游戏,准备了甲、乙两个口袋,其中甲口袋中放有标号为1,2,3,4,5的5个球,乙口袋中放有标号为1,2,3,4的4个球.游戏规则:甲从甲口袋摸一球,乙从乙口袋摸一球,摸出的两球所标数字之差(甲数字﹣乙数字)大于0时甲胜,小于0时乙胜,等于0时平局.你认为这个游戏规则对双方公平吗?请说明理由.若不公平,请你对本游戏设计一个对双方都公平的游戏规则.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD∽四边形A′B′C′D′,且AB∶BC∶CD∶DA=20∶15∶9∶8,四边形A′B′C′D′的周长为26,求四边形A′B′C′D′各边的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=30°,△CDE是等边三角形,点D在边AB上.

(1)如图1,当点E在边BC上时,求证DE=EB;
(2)如图2,当点E在△ABC内部时,猜想ED和EB数量关系,并加以证明;
(3)如图3,当点E在△ABC外部时,EH⊥AB于点H,过点E作GE∥AB,交线段AC的延长线于点G,AG=5CG,BH=3.求CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线PT与⊙O相交于点T,直线PO与⊙O相交于A,B两点.已知∠PTA=∠B.
(1)求证:PT是⊙O的切线;
(2)若PT=6,PA=4,求⊙O的半径;
(3)若PT=TB=![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为一圆洞门.工匠在建造过程中需要一根横梁AB和两根对称的立柱CE、DF来支撑,点A、B、C、D在⊙O上,CE⊥AB于E,DF⊥AB于F,且AB=2![]() ,EF=
,EF=![]() ,
,![]() =120°.
=120°.
(1)求出圆洞门⊙O的半径;
(2)求立柱CE的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用函数方法研究动点到定点的距离问题.
在研究一个动点P(x,0)到定点A(1,0)的距离S时,小明发现:
S与x的函数关系为S= 并画出图像如图:
并画出图像如图:

借助小明的研究经验,解决下列问题:
(1)写出动点P(x,0)到定点B(-2,0)的距离S的函数表达式,并求当x取何值时,S取最小值?
(2)设动点P(x,0)到两个定点M(1,0)、N(5,0)的距离和为y.
①随着x增大,y怎样变化?
②当x取何值时,y取最小值,y的最小值是多少?
③当x<1时,证明y随着x增大而变化的规律.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在平面直角坐标系中,直线![]() 交坐标轴于A、B两点,过点C(
交坐标轴于A、B两点,过点C(![]() ,0)作CD交AB于D,交
,0)作CD交AB于D,交![]() 轴于点E.且△COE≌△BOA.
轴于点E.且△COE≌△BOA.

(1)求B点坐标为 ;线段OA的长为 ;
(2)确定直线CD解析式,求出点D坐标;
(3)如图2,点M是线段CE上一动点(不与点C、E重合),ON⊥OM交AB于点N,连接MN.
①点M移动过程中,线段OM与ON数量关系是否不变,并证明;
②当△OMN面积最小时,求点M的坐标和△OMN面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com