
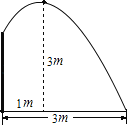
【题目】要修建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端安一个喷头,使喷出的抛物线形水柱在与水池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离中心3m.
(1)在给定的坐标系中画出示意图;
(2)求出水管的长度.
【答案】(1)详见解析;(2)水管长为2.25m.
【解析】
(1)以池中心为原点,竖直安装的水管为y轴,与水管垂直的为x轴建立直角坐标系;
(2)设抛物线的解析式为y=a(x﹣1)2+3(0≤x≤3),将(3,0)代入求得a值,则x=0时得的y值即为水管的长.
解:(1)建立以池中心为原点,竖直安装的水管为y轴,与水管垂直的为x轴建立直角坐标系;
(2)由于在距池中心的水平距离为1m时达到最高,高度为3m,
则设抛物线的解析式为:
y=a(x﹣1)2+3(0≤x≤3),
代入(3,0)求得:a=﹣![]() .
.
将a值代入得到抛物线的解析式为:
y=﹣![]() (x﹣1)2+3(0≤x≤3),
(x﹣1)2+3(0≤x≤3),
令x=0,则y=![]() =2.25.
=2.25.
故水管长为2.25m.


科目:初中数学 来源: 题型:
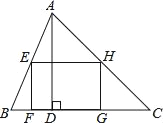
【题目】如图,矩形EFGH内接于△ABC,且边FG落在BC上,若AD⊥BC,BC=3,AD=2,EF=![]() EH.
EH.
(1)求证:△AEH∽△ABC;
(2)求矩形EFGH的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
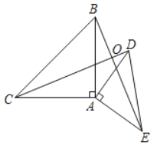
【题目】如图,△ABC与△ADE都是等腰直角三角形,连接CD、BE,CD、BE相交于点O,△BAE可看作是由△CAD顺时针旋转所得.
(1)旋转中心是 ,旋转角度是 ;
(2)判断CD与BE的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
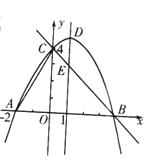
【题目】如图,抛物线![]() 与
与![]() 轴交于点C(O,4),与
轴交于点C(O,4),与![]() 轴交于点A和点B,其中点A的坐标为(-2,0),抛物线的对称轴
轴交于点A和点B,其中点A的坐标为(-2,0),抛物线的对称轴![]() 与抛物线交于点D,与直线BC交于点E.
与抛物线交于点D,与直线BC交于点E.
(1)求抛物线的解析式;
(2)若点F是直线BC上方的抛物线上的一个动点,是否存在点F使四边形ABFC的面积为17,若存在,求出点F的坐标;若不存在,请说明理由;
(3)平行于DE的一条动直线Z与直线BC相交于点P,与抛物线相交于点Q,若以D、E、P、Q为顶点的四边形是平行四边形,求点P的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() (m>0)与x轴的交点为A,B.
(m>0)与x轴的交点为A,B.
(1)求抛物线的顶点坐标;
(2)横、纵坐标都是整数的点叫做整点.
①当m=1时,求线段AB上整点的个数;
②若抛物线在点A,B之间的部分与线段AB所围成的区域内(包括边界)恰有6个整点,结合函数的图象,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是等边三角形ABC内的一点,且PA=6,PB=8,PC=10.
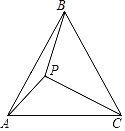
(1)尺规作图:作出将△PAC绕点A逆时针旋转60°后所得到的△P′AB(不要求写作法,但需保留作图痕迹).
(2)求点P与点P′之间的距离及∠APB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,顶点为点
,顶点为点![]() .
.
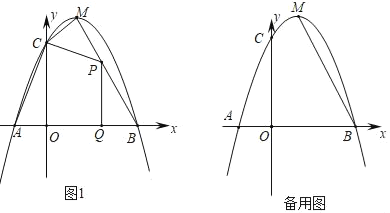
(1)求这条抛物线的解析式及直线![]() 的解析式;
的解析式;
(2)![]() 段
段![]() 上一动点(点
上一动点(点![]() 不与点
不与点![]() 、
、![]() 重合),过点
重合),过点![]() 向
向![]() 轴引垂线,垂足为
轴引垂线,垂足为![]() ,设
,设![]() 的长为
的长为![]() ,四边形
,四边形![]() 的面积为
的面积为![]() .求
.求![]() 与
与![]() 之间的函数关系式及自变量
之间的函数关系式及自变量![]() 的取值范围;
的取值范围;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 为等腰三角形?若存在,请直接写出点
为等腰三角形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实国务院房地产调控政策,使“居者有其屋”.某市加快了廉租房的建设力度,2013年市政府共投资3亿元人民币建设了廉租房12万平方米,2015年投资6.75亿元人民币建设廉租房,若在这两年内每年投资的增长率相同.
(1)求每年市政府投资的增长率;
(2)若这两年内的建设成本不变,问2015年建设了多少万平方米廉租房?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com