
【题目】如图,直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,已知
点,已知![]() 点的坐标为
点的坐标为![]() ,
,![]() 点坐标为
点坐标为![]() 。
。
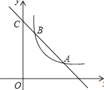
(1)求函数![]() 的表达式和
的表达式和![]() 点坐标;
点坐标;
(2)观察图像,当![]() 时,直接写出
时,直接写出![]() 的取值范围。
的取值范围。
科目:初中数学 来源: 题型:
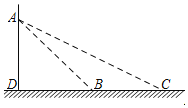
【题目】如图,一辆轿车在经过某路口的感应线B和C处时,悬臂灯杆上的电子警察拍摄到两张照片,两感应线之间距离BC为6.2m,在感应线B、C两处测得电子警察A的仰角分别为∠ABD=45°,∠ACD=28°.求电子警察安装在悬臂灯杆上的高度AD的长.(结果精确到0.1米)(参考数据:sin28°=0.47,cos28°=0.88,tan28°=0.53)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在不透明的袋子中有黑棋子10枚和白棋子若干(它们除颜色外都相同),现随机从中摸出10枚记下颜色后放回,这样连续做了10次,记录了如下的数据:
次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
黑棋数 | 1 | 3 | 0 | 2 | 3 | 4 | 2 | 1 | 1 | 3 |
根据以上数据,估算袋中的白棋子数量为( )
A. 60枚 B. 50枚 C. 40枚 D. 30枚
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店经市场调查,发现进价为40元的某新型文具每月的销售量y(件)与售价x(元)的相关信息如下:
售价x(元) | 60 | 70 | 80 | 90 | … |
销售量y(件) | 280 | 260 | 240 | 220 | … |
(1)试用你学过的函数来描述y与x的关系,这个函数可以是 (填“一次函数”、“反比例函数”或“二次函数”),并求这个函数关系式;
(2)当售价为多少元时,当月的销售利润最大,最大利润是多少;
(3)若获利不得高于进价的80%,那么售价定为多少元时,月销售利润达到最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
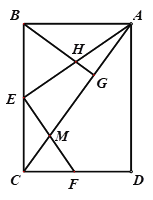
【题目】 如图,![]() 是矩形
是矩形![]() 的边
的边![]() 上的一点,AC是其对角线,连接AE,过点E作
上的一点,AC是其对角线,连接AE,过点E作![]() 交
交![]() 于点
于点![]() ,
, ![]() 交DC于点F,过点B作
交DC于点F,过点B作![]() 于点G,
于点G,![]() 交AE于点H.
交AE于点H.
(1)求证:![]() ∽
∽![]() ;
;
(2)求证:![]() ;
;
(3)若E是BC的中点,![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应“绿水青山就是金山银山”的号召,建设生态文明,某工厂自2019年1月开始限产并进行治污改造,其月利润![]() (万元)与月份
(万元)与月份![]() 之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的部分,下列选项错误的是( )
之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的部分,下列选项错误的是( )
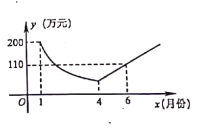
A.4月份的利润为![]() 万元
万元
B.污改造完成后每月利润比前一个月增加![]() 万元
万元
C.治污改造完成前后共有![]() 个月的利润低于
个月的利润低于![]() 万元
万元
D.9月份该厂利润达到![]() 万元
万元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某化工材料经销商购进一种化工材料若干千克,成本为每千克30元,物价部门规定其销售单价不低于成本价且不高于成本价的2倍,经试销发现,日销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元)符合一次函数关系,如图所示.
(元)符合一次函数关系,如图所示.
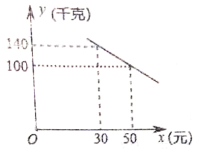
(1)求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)若在销售过程中每天还要支付其他费用500元,当销售单价为多少时,该公司日获利最大?最大获利是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
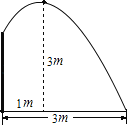
【题目】要修建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端安一个喷头,使喷出的抛物线形水柱在与水池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离中心3m.
(1)在给定的坐标系中画出示意图;
(2)求出水管的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的.连接BE、CF相交于点D.
(1)求证:BE=CF.
(2)当四边形ACDE为菱形时,求BD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com