
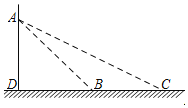
【题目】如图,一辆轿车在经过某路口的感应线B和C处时,悬臂灯杆上的电子警察拍摄到两张照片,两感应线之间距离BC为6.2m,在感应线B、C两处测得电子警察A的仰角分别为∠ABD=45°,∠ACD=28°.求电子警察安装在悬臂灯杆上的高度AD的长.(结果精确到0.1米)(参考数据:sin28°=0.47,cos28°=0.88,tan28°=0.53)
科目:初中数学 来源: 题型:
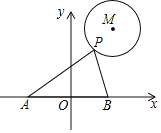
【题目】 如图,⊙M的半径为2,圆心M的坐标为(3,4),点P是⊙M上的任意一点,PA⊥PB,且PA、PB与x轴分别交于A、B两点,若点A、点B关于原点O对称,则AB的最小值为( )
A. 3B. 4C. 6D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
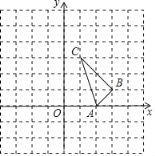
【题目】在平面直角坐标系中,已知A(2,0)、B(3,1)、C(1,3).
(1)画出△ABC沿x轴负方向平移2个单位后得到的△A1B1C1,并写出B1的坐标 ;
(2)以A1点为旋转中心,将△A1B1C1逆时针方向旋转90°得△A1B2C2,画出△A1B2C2,并写出C2的坐标 ;
(3)直接写出过B、B1、C2三点的圆的圆心坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件40元,售价为每件50元,每个月可卖出210件;如果每件商品的售价每上涨1元,则每个月少卖10件(每件售价不能高于65元),设每件商品的售价上涨![]() 元(
元(![]() 为正整数),每个月的销售利润为
为正整数),每个月的销售利润为![]() 元.
元.
(1)求![]() 与
与![]() 的函数关系式并直接写出自变量
的函数关系式并直接写出自变量![]() 的取值范围;
的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大月利润是多少元?
(3)每件商品的售价定为多少元时,每个月的利润恰为2 200元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一张长12dm,宽6dm的长方形纸板,将纸板四个角各剪去一个同样的边长为xdm的正方形,然后将四周突出部分折起,可制成一个无盖长方体纸盒.
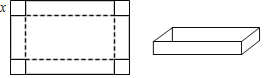
(1)无盖方盒盒底的长为 dm,宽为 dm(用含x的式子表示).
(2)若要制作一个底面积是40dm2的一个无盖长方体纸盒,求剪去的正方形边长x.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
如图1,在Rt△ABC和Rt△CDE中,∠ACB=∠DCE=90°,∠CAB=∠CDE=45°,点D时线段AB上一动点,连接BE.
填空:①![]() 的值为 ; ②∠DBE的度数为 .
的值为 ; ②∠DBE的度数为 .

(2)类比探究
如图2,在Rt△ABC和Rt△CDE中,∠ACB=∠DCE=90°,∠CAB=∠CDE=60°,点D是线段AB上一动点,连接BE.请判断![]() 的值及∠DBE的度数,并说明理由;
的值及∠DBE的度数,并说明理由;
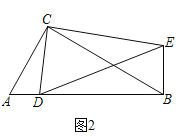
(3)拓展延伸
如图3,在(2)的条件下,将点D改为直线AB上一动点,其余条件不变,取线段DE的中点M,连接BM、CM,若AC=2,则当△CBM是直角三角形时,线段BE的长是多少?请直接写出答案.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() cm,
cm,![]() cm,点
cm,点![]() 从点
从点![]() 出发沿
出发沿![]() 以2cm/s的速度向终点
以2cm/s的速度向终点![]() 匀速运动,同时点
匀速运动,同时点![]() 从点
从点![]() 出发沿
出发沿![]() 以1 cm/s的速度向终点
以1 cm/s的速度向终点![]() 匀速运动,
匀速运动,![]() 、
、![]() 中有一点到达终点时,另一点随之停止运动.
中有一点到达终点时,另一点随之停止运动.
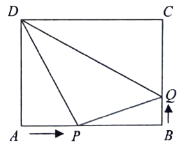
(1)几秒后,点![]() 、D的距离是点
、D的距离是点![]() 、
、![]() 的距离的2倍;
的距离的2倍;
(2)几秒后,PDQ是直角三角形;
(3)在运动过程中,经过 秒,以![]() 为圆心,
为圆心,![]() 为半径的⊙
为半径的⊙![]() 与对角线
与对角线![]() 相切.
相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
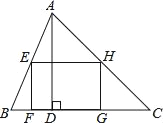
【题目】如图,矩形EFGH内接于△ABC,且边FG落在BC上,若AD⊥BC,BC=3,AD=2,EF=![]() EH.
EH.
(1)求证:△AEH∽△ABC;
(2)求矩形EFGH的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com