
【题目】如图是一张长12dm,宽6dm的长方形纸板,将纸板四个角各剪去一个同样的边长为xdm的正方形,然后将四周突出部分折起,可制成一个无盖长方体纸盒.
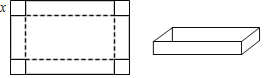
(1)无盖方盒盒底的长为 dm,宽为 dm(用含x的式子表示).
(2)若要制作一个底面积是40dm2的一个无盖长方体纸盒,求剪去的正方形边长x.
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() .
.
(1)该抛物线的对称轴是![]() ________.
________.
(2)该抛物线与![]() 轴交于点
轴交于点![]() ,点
,点![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,若此抛物线的对称轴上的点
,若此抛物线的对称轴上的点![]() 满足
满足![]() ,则点
,则点![]() 的纵坐标
的纵坐标![]() 的取值范围是________.
的取值范围是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
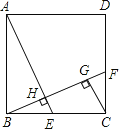
【题目】如图,在正方形ABCD中,E是BC上的一点,连结AE,作BF⊥AE,垂足为H,交CD于F,作CG∥AE,交BF于G.
求证:(1) CG=BH;(2)FC2=BF·GF;(3)![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)过点A(1,0),B(3,0)两点,与y轴交于点C,OC=3.
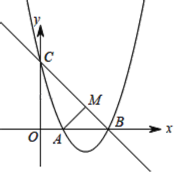

(1)求抛物线的解析式及顶点D的坐标;
(2)点P为抛物线在直线BC下方图形上的一动点,当△PBC面积最大时,求点P的坐标;
(3)若点Q为线段OC上的一动点,问:AQ+![]() QC是否存在最小值?若存在,求岀这个最小值;若不存在,请说明理由.
QC是否存在最小值?若存在,求岀这个最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,正方形ABCD的四个顶点坐标分别为A(-2,4),B(-2,-2),C(4,-2),D(4,4).
(1)填空:正方形的面积为_______;当双曲线![]() (k≠0)与正方形ABCD有四个交点时,k的取值范围是_______.
(k≠0)与正方形ABCD有四个交点时,k的取值范围是_______.
(2)已知抛物线L:![]() (a>0)顶点P在边BC上,与边AB,DC分别相交于点E,F,过点B的双曲线
(a>0)顶点P在边BC上,与边AB,DC分别相交于点E,F,过点B的双曲线![]() (k≠0)与边DC交于点N.
(k≠0)与边DC交于点N.
①点Q(m,-m2-2m+3)是平面内一动点,在抛物线L的运动过程中,点Q随m运动,分别求运动过程中点Q在最高位置和最低位置时的坐标.
②当点F在点N下方,AE=NF,点P不与B,C两点重合时,求![]() 的值.
的值.
③求证:抛物线L与直线![]() 的交点M始终位于
的交点M始终位于![]() 轴下方.
轴下方.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一辆轿车在经过某路口的感应线B和C处时,悬臂灯杆上的电子警察拍摄到两张照片,两感应线之间距离BC为6.2m,在感应线B、C两处测得电子警察A的仰角分别为∠ABD=45°,∠ACD=28°.求电子警察安装在悬臂灯杆上的高度AD的长.(结果精确到0.1米)(参考数据:sin28°=0.47,cos28°=0.88,tan28°=0.53)
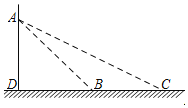
查看答案和解析>>
科目:初中数学 来源: 题型:
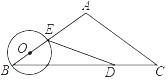
【题目】如图,等腰△ABC中,AB=AC=5cm,BC=8cm.动点D从点C出发,沿线段CB以2cm/s的速度向点B运动,同时动点O从点B出发,沿线段BA以1cm/s的速度向点A运动,当其中一个动点停止运动时另一个动点也随时停止.设运动时间为t(s),以点O为圆心,OB长为半径的⊙O与BA交于另一点E,连接ED.当直线DE与⊙O相切时,t的取值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
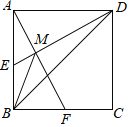
【题目】如图,已知E,F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M.则下列结论:①∠AME=90°,②∠BAF=∠EDB,③AM=![]() MF,④ME+MF=
MF,④ME+MF=![]() MB.其中正确结论的有( )
MB.其中正确结论的有( )
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
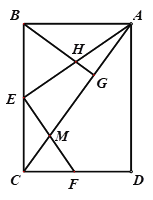
【题目】 如图,![]() 是矩形
是矩形![]() 的边
的边![]() 上的一点,AC是其对角线,连接AE,过点E作
上的一点,AC是其对角线,连接AE,过点E作![]() 交
交![]() 于点
于点![]() ,
, ![]() 交DC于点F,过点B作
交DC于点F,过点B作![]() 于点G,
于点G,![]() 交AE于点H.
交AE于点H.
(1)求证:![]() ∽
∽![]() ;
;
(2)求证:![]() ;
;
(3)若E是BC的中点,![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com