
【题目】如图,在矩形![]() 中,
中,![]() cm,
cm,![]() cm,点
cm,点![]() 从点
从点![]() 出发沿
出发沿![]() 以2cm/s的速度向终点
以2cm/s的速度向终点![]() 匀速运动,同时点
匀速运动,同时点![]() 从点
从点![]() 出发沿
出发沿![]() 以1 cm/s的速度向终点
以1 cm/s的速度向终点![]() 匀速运动,
匀速运动,![]() 、
、![]() 中有一点到达终点时,另一点随之停止运动.
中有一点到达终点时,另一点随之停止运动.
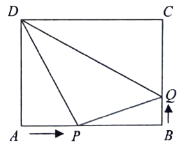
(1)几秒后,点![]() 、D的距离是点
、D的距离是点![]() 、
、![]() 的距离的2倍;
的距离的2倍;
(2)几秒后,PDQ是直角三角形;
(3)在运动过程中,经过 秒,以![]() 为圆心,
为圆心,![]() 为半径的⊙
为半径的⊙![]() 与对角线
与对角线![]() 相切.
相切.
【答案】(1)![]() ;(2)
;(2)![]() 或11-
或11-![]() ;(3)
;(3)![]() .
.
【解析】
(1)设t秒后点P、D的距离是点P、Q距离的2倍,即PD=2PQ,根据勾股定理得![]() ,
,![]() ,利用
,利用![]() ,列方程:
,列方程:![]() ,即可解得t的值
,即可解得t的值
(2)设t秒后,△DPQ是直角三角形分两种情况进行讨论:当∠DPQ=90°时,可证
△ADP![]() △BPQ,利用
△BPQ,利用![]() 列方程即可求出t的值;当∠DQP=90°时,可证
列方程即可求出t的值;当∠DQP=90°时,可证
△CDQ![]() △BQP,利用
△BQP,利用![]() 列方程即可求出t的值.
列方程即可求出t的值.
(3)连接BD,设⊙P与BD相切于m,连接PM,可知AP=PM=2t,BP=8-2t,
可得![]() ,在
,在![]() ,列出方程:
,列出方程:![]() ,
,
即可求出t的值.
解:
(1)设t秒后点P、D的距离是点P、Q距离的2倍,即PD=2PQ,
∵四边形ABCD是矩形,
∴∠A=∠B=90°,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
解得![]() ;
;
∵![]() ,
,
∴![]() .
.
(2)设t秒后,△DPQ是直角三角形,
当∠DPQ=90°时,∠ADP=∠BPQ,
∵∠A=∠B=90°,
∴△ADP![]() △BPQ,
△BPQ,
∴![]() ,
,
∴![]() ,
,
解得: ![]() (舍去),
(舍去),
当∠DQP=90°时,∠CDQ=∠BQP,
∵∠B=∠C=90°,
∴△CDQ![]() △BQP,
△BQP,
∴![]() ,
,
∴![]() ,
,
解得: ![]() (舍去),
(舍去),
答:当运动时间为![]() 或11-
或11-![]() 秒时,△DPQ是直角三角形;
秒时,△DPQ是直角三角形;
(3)连接BD,设⊙P与BD相切于m,连接PM,
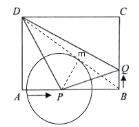
∴AP=PM=2t,
∴BP=8-2t,
∵AD=6,AB=8,
∴BD=10,
∴![]() ,
,
在![]() ,
,
∴![]() ,
,
解得t=![]() .
.
故答案为![]() .
.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,D、E分别是AB,AC的中点,作∠B的角平分线
(1)如图1,若∠B的平分线恰好经过点E,猜想△ABC是怎样的特殊三角形,并说明理由;
(2)如图2,若∠B的平分线交线段DE于点F,已知AB=8,BC=10,求EF的长度;
(3)若∠B的平分线交直线DE于点F,直接写出AB、BC、EF三者之间的数量关系。


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)过点A(1,0),B(3,0)两点,与y轴交于点C,OC=3.
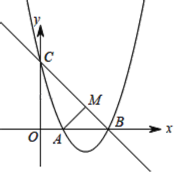

(1)求抛物线的解析式及顶点D的坐标;
(2)点P为抛物线在直线BC下方图形上的一动点,当△PBC面积最大时,求点P的坐标;
(3)若点Q为线段OC上的一动点,问:AQ+![]() QC是否存在最小值?若存在,求岀这个最小值;若不存在,请说明理由.
QC是否存在最小值?若存在,求岀这个最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一辆轿车在经过某路口的感应线B和C处时,悬臂灯杆上的电子警察拍摄到两张照片,两感应线之间距离BC为6.2m,在感应线B、C两处测得电子警察A的仰角分别为∠ABD=45°,∠ACD=28°.求电子警察安装在悬臂灯杆上的高度AD的长.(结果精确到0.1米)(参考数据:sin28°=0.47,cos28°=0.88,tan28°=0.53)
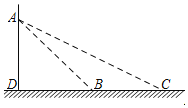
查看答案和解析>>
科目:初中数学 来源: 题型:
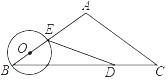
【题目】如图,等腰△ABC中,AB=AC=5cm,BC=8cm.动点D从点C出发,沿线段CB以2cm/s的速度向点B运动,同时动点O从点B出发,沿线段BA以1cm/s的速度向点A运动,当其中一个动点停止运动时另一个动点也随时停止.设运动时间为t(s),以点O为圆心,OB长为半径的⊙O与BA交于另一点E,连接ED.当直线DE与⊙O相切时,t的取值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知E,F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M.则下列结论:①∠AME=90°,②∠BAF=∠EDB,③AM=![]() MF,④ME+MF=
MF,④ME+MF=![]() MB.其中正确结论的有( )
MB.其中正确结论的有( )
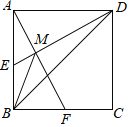
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在不透明的袋子中有黑棋子10枚和白棋子若干(它们除颜色外都相同),现随机从中摸出10枚记下颜色后放回,这样连续做了10次,记录了如下的数据:
次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
黑棋数 | 1 | 3 | 0 | 2 | 3 | 4 | 2 | 1 | 1 | 3 |
根据以上数据,估算袋中的白棋子数量为( )
A. 60枚 B. 50枚 C. 40枚 D. 30枚
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某化工材料经销商购进一种化工材料若干千克,成本为每千克30元,物价部门规定其销售单价不低于成本价且不高于成本价的2倍,经试销发现,日销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元)符合一次函数关系,如图所示.
(元)符合一次函数关系,如图所示.
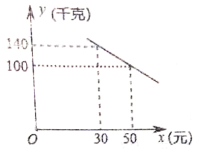
(1)求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)若在销售过程中每天还要支付其他费用500元,当销售单价为多少时,该公司日获利最大?最大获利是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com