
【题目】如图,P是等边三角形ABC内的一点,且PA=6,PB=8,PC=10.
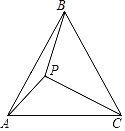
(1)尺规作图:作出将△PAC绕点A逆时针旋转60°后所得到的△P′AB(不要求写作法,但需保留作图痕迹).
(2)求点P与点P′之间的距离及∠APB的度数.
【答案】(1)详见解析;(2)PP′=6,∠APB=150°.
【解析】
(1)作等边三角形APP′,连接P′B,则△P′AB是所求作的三角形;
(2)根据旋转的性质得到∠PAP′=60°,PA=P′A=6,P′B=PC=10,利用等边三角形的判定方法得到△PAP′为等边三角形,再根据等边三角形的性质有PP′=PA=6,∠P′PA=60°,由于PP′2+PB2=P′B2,根据勾股定理的逆定理得到△BPP′为直角三角形,且∠BPP′=90°,则∠APB=∠P′PB+∠BPP′=60°+90°=150°.
解:(1)将△PAC绕点A逆时针旋转60°后所得到的△P′AB如图:

(2)如图,∵△PAC绕点A逆时针旋转60°后,得到△P′AB,
∴∠PAP′=60°,PA=P′A=6,P′B=PC=10,
∴△PAP′为等边三角形,
∴PP′=PA=6,∠P′PA=60°,
在△BPP′中,P′B=10,PB=8,PP′=6,
∵62+82=102,
∴PP′2+PB2=P′B2,
∴△BPP′为直角三角形,且∠BPP′=90°,
∴∠APB=∠P′PB+∠BPP′=60°+90°=150°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在不透明的袋子中有黑棋子10枚和白棋子若干(它们除颜色外都相同),现随机从中摸出10枚记下颜色后放回,这样连续做了10次,记录了如下的数据:
次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
黑棋数 | 1 | 3 | 0 | 2 | 3 | 4 | 2 | 1 | 1 | 3 |
根据以上数据,估算袋中的白棋子数量为( )
A. 60枚 B. 50枚 C. 40枚 D. 30枚
查看答案和解析>>
科目:初中数学 来源: 题型:
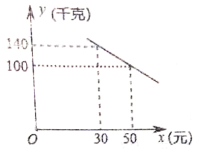
【题目】我市某化工材料经销商购进一种化工材料若干千克,成本为每千克30元,物价部门规定其销售单价不低于成本价且不高于成本价的2倍,经试销发现,日销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元)符合一次函数关系,如图所示.
(元)符合一次函数关系,如图所示.
(1)求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)若在销售过程中每天还要支付其他费用500元,当销售单价为多少时,该公司日获利最大?最大获利是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
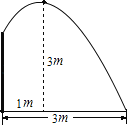
【题目】要修建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端安一个喷头,使喷出的抛物线形水柱在与水池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离中心3m.
(1)在给定的坐标系中画出示意图;
(2)求出水管的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图C是线段BD上一点,分别以BC、CD为边在BD同侧作等边△ABC和等边△CDE,AD交CE于F,BE交AC于G,则图中可通过旋转而相互得到的三角形对数有( )

A.1对B.2对C.3对D.4对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四位同学在研究函数y=x2+bx+c(b,c是常数)时,甲发现当x=1时,函数有最小值;乙发现﹣1是方程x2+bx+c=0的一个根;丙发现函数的最小值为3;丁发现当x=2时,y=4,已知这四位同学中只有一位发现的结论是错误的,则该同学是( )
A. 甲 B. 乙 C. 丙 D. 丁
查看答案和解析>>
科目:初中数学 来源: 题型:
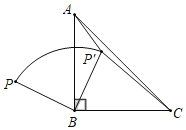
【题目】如图,点P是等腰Rt△ABC外一点,把线段BP绕点B顺时针旋转90°得到线段BP',已知∠AP'B=135°,P'A:P'C=1:3,则P'A:PB=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的.连接BE、CF相交于点D.
(1)求证:BE=CF.
(2)当四边形ACDE为菱形时,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国庆期间某旅游点一家商铺销售一批成本为每件50元的商品,规定销售单价不低于成本价,又不高于每件70元,销售量y(件)与销售单价x(元)的关系可以近似的看作一次函数(如图).
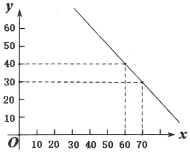
(1)请直接写出y关于x之间的关系式 ;
(2)设该商铺销售这批商品获得的总利润(总利润=总销售额一总成本)为P元,求P与x之间的函数关系式,并写出自变量x的取值范围;根据题意判断:当x取何值时,P的值最大?最大值是多少?
(3)若该商铺要保证销售这批商品的利润不能低于400元,求销售单价x(元)的取值范围是 .(可借助二次函数的图象直接写出答案)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com