
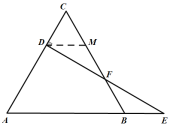
【题目】如图,等边三角形ABC中,D为AC上一点,E为AB延长线上一点,DE⊥AC交BC于点F,且DF=EF.
(1)求证:CD=BE;
(2)若AB=12,试求BF的长.

【答案】(1)证明见解析;(2)4.
【解析】
(1)先作DM∥AB,交CF于M,可得△CDM为等边三角形,再判定△DMF≌△EBF,最后根据全等三角形的性质以及等边三角形的性质,得出结论;
(2)根据CD⊥AC,∠A=60°=∠ABC,可得∠E=∠BFE=∠DFM=∠FDM=30°,由此得出CM=MF=BF=![]() BC,最后根据AB=12即可求得BF的长.
BC,最后根据AB=12即可求得BF的长.
(1)证明:如图,作DM∥AB,交CB于M,则∠DMF=∠EBF.
∵△ABC是等边三角形,
∴∠C=60°=∠CDM=∠CMD,
∴△CDM是等边三角形,
∴CD=DM.
在△DMF和△EBF中,
∠DMF=∠EBF,
∠DFM=∠EFB,
DF=EF,
∴△DMF≌△EBF(AAS).
∴DM=BE,
∴CD=BE.
(2)解:∵ED⊥AC,∠A=60°=∠ABC,
∴∠E=∠BFE=∠DFM=∠FDM=30°,
∴BE=BF,DM=FM.
由(1)知△DMF≌△EBF,
∴MF=BF,
∴CM=MF=BF.
又∵AB=BC=12,
∴CM=MF=BF=4.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】为更新果树品种,某果园计划新购进A、B两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中A种树苗的单价为7元/棵,购买B种苗所需费用y(元)与购买数量x(棵)之间存在如图所示的函数关系.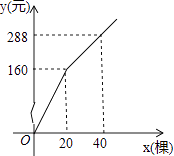
(1)求y与x的函数关系式;
(2)若在购买计划中,B种树苗的数量不超过35棵,但不少于A种树苗的数量,请设计购买方案,使总费用最低,并求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,每个小正方形的边长为1,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.根据下列条件,利用网格点和直尺画图:
(1)补全△A′B′C′;
(2)作出△ABC的中线CD;
(3)画出BC边上的高线AE;
(4)若△ABC与△ABE面积相等,则图中满足条件且异于点C的格点E共有 个.(注:格点指网格线的交点)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的边AC与⊙O相交于C、D两点,且经过圆心O,边AB与⊙O相切,切点为B.已知∠A=30°,则∠C的大小是( )
A.30°
B.45°
C.60°
D.40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将数轴按如图所示从某一点开始折出一个等边三角形ABC,设点A表示的数为x﹣3,点B表示的数为2x+1,点C表示的数为﹣4,若将△ABC向右滚动,则x的值等于_____,数字2012对应的点将与△ABC的顶点_____重合.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一张长方形纸片ABCD沿EF折叠后,点A落在CD边上的点A '处,点B落在点B '处,若∠1=115° ,则图中∠2的度数为( )
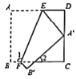
A. 40°B. 45°C. 50°D. 60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车油箱内有油a升,从某地出发,每行驶1小时耗油6升,若设剩余油量为Q升,行驶时间为t/小时,根据以上信息回答下列问题:
(1)开始时,汽车的油量a=_____升;
(2)在_____小时汽车加油,加了_____升,
写出加油前Q与t之间的关系式______;
(3)这辆汽车行驶8小时,剩余油量多少升?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD=BC=12,AB=CD,BD=15,点E从D点出发,以每秒4个单位的速度沿D→A→D匀速移动,点F从点C出发,以每秒1个单位的速度沿CB向点B作匀速移动,点G从点B出发沿BD向点D匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动,假设移动时间为t秒.

(1)试说明:AD∥BC;
(2)在移动过程中,小明发现有△DEG与△BFG全等的情况出现,请你探究这样的情况会出现几次?并分别求出此时的移动时间t和G点的移动距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于![]() ,
, ![]() 的方程组
的方程组![]()
(1)请写出方程![]() 的所有正整数解;
的所有正整数解;
(2)若方程组的解满足![]() ,求
,求![]() 的值;
的值;
(3)无论实数![]() 取何值,方程
取何值,方程![]() 总有一个公共解,你能把求出这个公共解吗?
总有一个公共解,你能把求出这个公共解吗?
(4)如果方程组有整数解,求整数![]() 的值。
的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com