
【题目】如图,在直角坐标系内,O为原点,点A的坐标为(10,0),点B在第一象限内,BO=5,sin∠BOA=![]() . 求:(1)点B的坐标;(2)cos∠BAO的值.
. 求:(1)点B的坐标;(2)cos∠BAO的值.
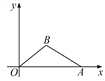
【答案】(1)点B的坐标为(4,3);(2)cos∠BAO=![]() .
.
【解析】试题分析:(1)作BH⊥OA, 垂足为H,在Rt△OHB中,根据锐角三角函数的定义及已知条件求得BH的长,再根据勾股定理求得OH的长,即可得点B的坐标;(2)先求得AH的长,在Rt△AHB中,根据勾股定理求得AB的长,根据锐角三角函数的定义即可求得cos∠BAO的值.
试题解析:
(1)如图所示,作BH⊥OA, 垂足为H.
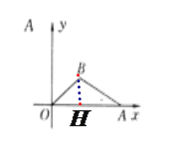
在Rt△OHB中,∵BO=5,sin∠BOA=![]() ,∴BH=3,∴OH=4,∴点B的坐标为(4,3).
,∴BH=3,∴OH=4,∴点B的坐标为(4,3).
(2)∵OA=10,OH=4,∴AH=6.在Rt△AHB中,∵BH=3,∴AB=![]() ,∴cos∠BAO=
,∴cos∠BAO=![]() =
= ![]() .
.


科目:初中数学 来源: 题型:
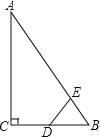
【题目】如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t的值为( )
A.2B.2.5或3.5
C.3.5或4.5D.2或3.5或4.5
查看答案和解析>>
科目:初中数学 来源: 题型:
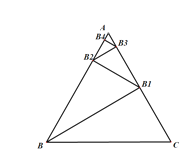
【题目】如图,△ABC是一个边长为1的等边三角形,BB1是△ABC的高,B1B2是△ABB1的高,B2B3是△AB1B2的高,……Bn-1Bn是△ABn-2Bn-1的高,则B4B5的长是________,猜想Bn-1Bn的长是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一座拱桥是圆弧形,它的跨度AB=60米,拱高PD=18米.
(1)求圆弧所在的圆的半径r的长;
(2)当洪水泛滥到跨度只有30米时,要采取紧急措施,若拱顶离水面只有4米,即PE=4米时,是否要采取紧急措施?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班数学兴趣小组利用数学活动课时间测量位于烈山山顶的炎帝雕像高度,已知烈山坡面与水平面的夹角为30°,山高857.5尺,组员从山脚D处沿山坡向着雕像方向前进1620尺到达E点,在点E处测得雕像顶端A的仰角为60°,求雕像AB的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的边
的边![]() 、
、![]() 在坐标轴上,点
在坐标轴上,点![]() 坐标
坐标![]() ,将正方形
,将正方形![]() 绕点
绕点![]() 顺时针旋转角度
顺时针旋转角度![]() ,得到正方形
,得到正方形![]() ,
,![]() 交线段
交线段![]() 于点
于点![]() ,
,![]() 的延长线交线段
的延长线交线段![]() 于点
于点![]() ,连
,连![]() 、
、![]() .
.
(1)求证:![]() ;
;
(2)求![]() 的度数,并判断线段
的度数,并判断线段![]() 、
、![]() 、
、![]() 之间的数量关系,说明理由;
之间的数量关系,说明理由;
(3)当![]() 时,求直线
时,求直线![]() 的解析式.
的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,△ABC是正三角形,△BDC是顶角∠BDC=120°的等腰三角形,以D为顶点作一个60°角,角两边分别交AB,AC边于M,N两点,连接MN.

(1)探究:线段BM,MN,NC之间的关系,并加以证明。
(2)若点M是AB的延长线上的一点,N是CA的延长线上的点,其它条件不变,请你再探线段BM,MN,NC之间的关系,在图②中画出图形,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级开展征文活动,征文主题只能从“爱国”“敬业”“诚信”“友善”四个主题中选择一个,七年级每名学生按要求都上交了一份征文,学校为了解选择各种征文主题的学生人数,随机抽取了部分征文进行了调查,根据调查结果绘制成如下两幅不完整的统计图.
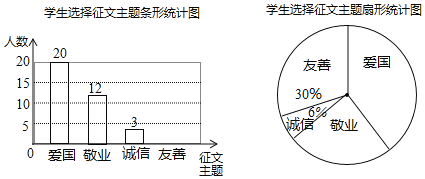
(1)将上面的条形统计图补充完整;
(2)在扇形统计图中,选择“爱国”主题所对应的圆心角是多少度?
(3)如果该校七年级共有1200名考生,请估计选择以“友善”为主题的七年级学生有多少名?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com