
 如图,矩形ABCD中,AB=5,BC=3,点E、F分别在边AB,CD上,连接EF,将∠BEF对折,点B落在直线EF上的点B′处,得折痕EM;将∠AEF对折,点A落在直线EF上的点A′处,得折痕EN,当M,N分别在边BC,AD上时,若令AN的长度为y,AE的长度为x,则y关于x的函数解析式是y=-$\frac{1}{3}$x2+$\frac{5}{3}$x.
如图,矩形ABCD中,AB=5,BC=3,点E、F分别在边AB,CD上,连接EF,将∠BEF对折,点B落在直线EF上的点B′处,得折痕EM;将∠AEF对折,点A落在直线EF上的点A′处,得折痕EN,当M,N分别在边BC,AD上时,若令AN的长度为y,AE的长度为x,则y关于x的函数解析式是y=-$\frac{1}{3}$x2+$\frac{5}{3}$x. 分析 由折叠的性质得:∠AEN=∠A'EN,∠BEC=∠B'EC,证出∠CEN=90°,得出∠AEN+∠BEC=90°,由矩形的性质得出∠A=∠B=90°,由直角三角形的性质得出∠AEN+∠ANE=90°,证出∠ANE=∠BEC,得出△AEN∽△BCE,由相似三角形的对应边成比例即可得出结果.
解答 解:由折叠的性质得:∠AEN=∠A'EN,∠BEC=∠B'EC,
∵∠AEB=180°,
∴∠CEN=$\frac{1}{2}$×180°=90°,
∴∠AEN+∠BEC=90°,
∵四边形ABCD是矩形,
∴∠A=∠B=90°,
∴∠AEN+∠ANE=90°,
∴∠ANE=∠BEC,
∴△AEN∽△BCE,
∴$\frac{AE}{BC}=\frac{AN}{BE}$,即$\frac{x}{3}=\frac{y}{5-x}$,
∴y=-$\frac{1}{3}$x2+$\frac{5}{3}$x;
故答案为:y=-$\frac{1}{3}$x2+$\frac{5}{3}$x.
点评 本题考查了矩形的性质、折叠的性质、直角三角形的性质、相似三角形的判定与性质;熟练掌握折叠的性质和矩形的性质,证明三角形相似是解决问题的关键.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:解答题
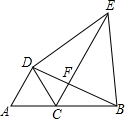 如图,点C在线段AB上,△DAC和△DBE都是等边三角形.
如图,点C在线段AB上,△DAC和△DBE都是等边三角形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x=1 | B. | x=2 | C. | x=0 | D. | x=-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{1}{3}$x-5=4,得$\frac{1}{3}$x=4+5 | B. | 5y-3y+y=9,得(5-3)y=9 | ||
| C. | x+7=26,得x=19 | D. | -5x=20,得x=-$\frac{5}{20}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 20+3+5-7 | B. | -20-3-5-7 | C. | -20-3+5+7 | D. | -20-3-5+7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com