
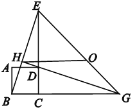
【题目】如图,四边形ABCD是正方形,ΔECG是等腰直角三角形,∠BGE的平分线过点D交BE 于H,O是EG的中点,对于下面四个结论:①GH⊥BE;②OH∥BG,且![]() ;③
;③![]() ;④△EBG的外接圆圆心和它的内切圆圆心都在直线HG上.其中表述正确的个数是( )
;④△EBG的外接圆圆心和它的内切圆圆心都在直线HG上.其中表述正确的个数是( )
A.1B.2C.3D.4
【答案】D
【解析】
①由四边形ABCD是正方形,△ECG是等腰直角三角形,得出△BCE≌△DCG,推出∠BEC+∠HDE=90°,从而得出GH⊥BE;
②由GH是∠EGC的平分线,得出△BGH≌△EGH,再由O是EG的中点,利用中位线定理,得出OH∥BG,且![]() ;
;
③由(2)得BG=EG,设CG=x,则CE=x,根据勾股定理得EG=![]() x,所以BG=
x,所以BG=![]() x,从而得到BC=(
x,从而得到BC=(![]() -1)x,根据正方形面积公式和等腰直角三角形面积公式可以得到S正方形ABCD=(3-2
-1)x,根据正方形面积公式和等腰直角三角形面积公式可以得到S正方形ABCD=(3-2![]() )x2,S△ECG=
)x2,S△ECG=![]() x2,进而求出
x2,进而求出![]() ;
;
④三角形的外接圆的圆心是三条边的垂直平分线的交点,三角形的内切圆是的圆心是三个角的平分线的交点.由(2)得BG=EG,由(1)得GH⊥BE,因为GH平分∠BGE,所以GH是BE边上的垂直平分线,所以△EBG的外接圆圆心和内切圆圆心在直线HG上.
解:①∵四边形ABCD是正方形,△ECG是等腰直角三角形
∴BC=CD,CE=CG,∠BCE=∠DCG=90°
在△BCE和△DCG中,

∴△BCE≌△DCG(SAS)
∴∠BEC=∠BGH
∵∠BGH+∠CDG=90°,∠CDG=∠HDE
∴∠BEC+∠HDE=90°
∴GH⊥BE
故①正确;
②∵GH是∠EGC的平分线
∴∠BGH=∠EGH
在△BGH和△EGH中,
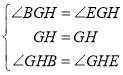
∴△BGH≌△EGH(ASA)
∴BH=EH
∵O是EG的中点
∴HO是△EBG的中位线
∴OH∥BG,且![]()
故②正确;
③由(2)得△BGH≌△EGH
∴BG=EG
在等腰直角三角形ECG中,设CG=x,则CE=x
∴EG=![]() =
=![]() x
x
∴BG=![]() x
x
∴BC=BG-CG=![]() x-x=(
x-x=(![]() -1)x
-1)x
∴S正方形ABCD=BC2=[(![]() -1)x]2 =(3-2
-1)x]2 =(3-2![]() )x2
)x2
S△ECG=![]()
![]() CG
CG![]() CE=
CE=![]() x2
x2
∴S正方形ABCD∶S△ECG=(3-2![]() )x2∶
)x2∶![]() x2=(6-4
x2=(6-4![]() )∶1
)∶1
故③正确;
④由(2)得BG=EG,由(1)得GH⊥BE
∵GH平分∠BGE,
∴GH是BE边上的垂直平分线
∵三角形的外接圆的圆心是三条边的垂直平分线的交点,三角形的内切圆是的圆心是三个角的平分线的交点.
∴△EBG的外接圆圆心和内切圆圆心在直线HG上
故④正确.
故选D.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
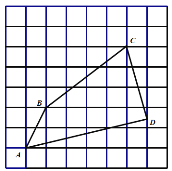
【题目】如图,在每个小正方形的边长为的网格中,点![]() 均在格点上,
均在格点上,![]() 为小正方形边中点.
为小正方形边中点.
(1)![]() 的长等于 ______;
的长等于 ______;
(2)请在如图所示的网格中,用无刻度的直尺,画出一个点![]() ,使其满足
,使其满足![]() 说明点
说明点![]() 的位置是如何找到的(不要求证明)______.
的位置是如何找到的(不要求证明)______.
查看答案和解析>>
科目:初中数学 来源: 题型:
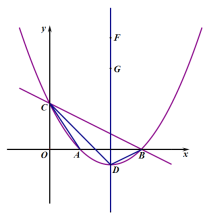
【题目】如图所示,抛物线y![]() x2bxc与直线y
x2bxc与直线y![]() x3分别交于x轴,y轴上的B,C两点,设该抛物线与x轴的另一个交点为A,顶点为D,连接CD交x轴于点E.
x3分别交于x轴,y轴上的B,C两点,设该抛物线与x轴的另一个交点为A,顶点为D,连接CD交x轴于点E.
(1)求该抛物线的函数表达式;
(2)求该抛物线的对称轴和D点坐标;
(3)点F,G是对称轴上两个动点,且FG=2,点F在点G的上方,请直接写出四边形ACFG的周长的最小值;
(4)连接BD,若P在y轴上,且∠PBC=∠DBA+∠DCB,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD边长为4,∠A=60°,M是AD边的中点,N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C,则A′C的最小值是( )

A.2![]() B.
B.![]() +1C.2
+1C.2![]() ﹣2D.3
﹣2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某货站传送货物的平面示意图,AD与地面的夹角为60°,为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°变成37°,因此传送带的落地点由点B到点C向前移动了2米.

(1)求点A与地面的高度;
(2)如果需要在货物着地点C的左侧留出2米,那么请判断距离D点14米的货物2是否需要挪走,并说明理由.(sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张用4张相同的小纸条做成甲、乙、丙、丁4支签,放在一个盒子中,搅匀后先从盒子中任意抽出1支签(不放回),再从剩余的3支签中任意抽出1支签.
(1)小张第一次抽到的是乙签的概率是 ;
(2)求抽出的两支签中,1支为甲签、1支为丙签的概率(用画树状图或列表法求解).
查看答案和解析>>
科目:初中数学 来源: 题型:
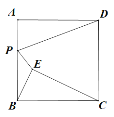
【题目】如图,已知正方形ABCD的边长为8,点E是正方形内部一点,连接BE,CE,且∠ABE=∠BCE,点P是AB边上一动点,连接 PD,PE,则PD+PE长度的最小值为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=![]() x2+bx+c过点A(3, 0)、点B(0, 3).点M(m, 0)在线段OA上(与点A、O不重合),过点M作x轴的垂线与线段AB交于点P,与抛物线交于点Q,联结BQ.
x2+bx+c过点A(3, 0)、点B(0, 3).点M(m, 0)在线段OA上(与点A、O不重合),过点M作x轴的垂线与线段AB交于点P,与抛物线交于点Q,联结BQ.
(1)求抛物线表达式;
(2)联结OP,当∠BOP=∠PBQ时,求PQ的长度;
(3)当△PBQ为等腰三角形时,求m的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com