
【题目】如图所示,抛物线y![]() x2bxc与直线y
x2bxc与直线y![]() x3分别交于x轴,y轴上的B,C两点,设该抛物线与x轴的另一个交点为A,顶点为D,连接CD交x轴于点E.
x3分别交于x轴,y轴上的B,C两点,设该抛物线与x轴的另一个交点为A,顶点为D,连接CD交x轴于点E.
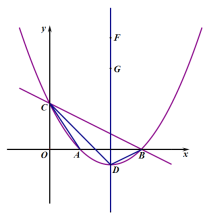
(1)求该抛物线的函数表达式;
(2)求该抛物线的对称轴和D点坐标;
(3)点F,G是对称轴上两个动点,且FG=2,点F在点G的上方,请直接写出四边形ACFG的周长的最小值;
(4)连接BD,若P在y轴上,且∠PBC=∠DBA+∠DCB,请直接写出点P的坐标.
【答案】(1)![]() ;(2)直线
;(2)直线![]() ;(3)
;(3)![]() ;(4)点P的坐标为
;(4)点P的坐标为![]() 或
或![]()
【解析】
(1)先根据直线![]() 求出B,C的坐标,然后利用待定系数法求抛物线的表达式即可;
求出B,C的坐标,然后利用待定系数法求抛物线的表达式即可;
(2)将抛物线的表达式变为顶点式,即可得到对称轴和D点坐标;
(3)因为AC,FG的值固定,所以只需找到![]() 的最小值即可,过点C作抛物线对称轴
的最小值即可,过点C作抛物线对称轴![]() 的对称点
的对称点![]() ,将
,将![]() 向下平移2个单位使F与点G重合,得到
向下平移2个单位使F与点G重合,得到![]() ,则
,则![]() ,当
,当![]() 三点共线时,
三点共线时,![]() 最小,最小值即为
最小,最小值即为![]() 的长度,通过勾股定理求出
的长度,通过勾股定理求出![]() 的值即可求解;
的值即可求解;
(4)分两种情况:当点P在y轴正半轴时和当点P在y轴负半轴时,首先通过锐角三角函数得出![]() ,从而得出
,从而得出![]() ,设
,设![]() ,则
,则![]() ,通过
,通过![]() 建立一个关于m的方程解方程即可求出PC的值,进而OP的长度即可,则P的坐标可求.
建立一个关于m的方程解方程即可求出PC的值,进而OP的长度即可,则P的坐标可求.
解:(1)令![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() ,解得
,解得![]() ,
,
![]() ,
,
将点![]() 代入
代入![]() 中得,
中得,
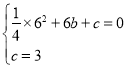 ,
,
解得![]()
∴抛物线的解析式为![]() ;
;
(2)∵![]() ,
,
∴抛物线的对称轴为![]() ,
,![]() ;
;
(3)∵抛物线的对称轴为![]() ,
,![]() ,
,
![]() ,
,
∵![]() ,
,
![]()
∵四边形ACFG的周长为![]() ,而
,而![]() ,
,
∴只需找到![]() 的最小值即可,
的最小值即可,
过点C作抛物线对称轴![]() 的对称点
的对称点![]() ,将
,将![]() 向下平移2个单位使F与点G重合,得到
向下平移2个单位使F与点G重合,得到![]() ,则
,则![]() ,
,
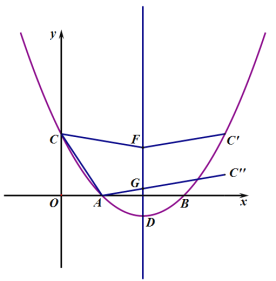
当![]() 三点共线时,
三点共线时,![]() 最小,最小值即为
最小,最小值即为![]() 的长度,
的长度,
![]() ,抛物线对称轴为
,抛物线对称轴为![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴四边形ACFG的周长的最小值为![]() ;
;
(4)如图,当点P在y轴正半轴时,过点P作![]() 交BC的延长线于点Q,
交BC的延长线于点Q,
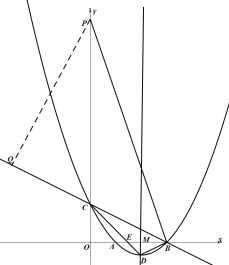
∵![]() ,
,
![]() .
.
设直线![]() 的解析式为
的解析式为![]() ,
,
将![]() 代入解析式中得
代入解析式中得
![]() ,
,
解得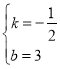 ,
,
∴直线CB解析式为![]() ,
,
令![]() ,则
,则![]() ,解得
,解得![]() ,
,
∴![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
设![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,
解得![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
当点P在y轴负半轴时,如图,
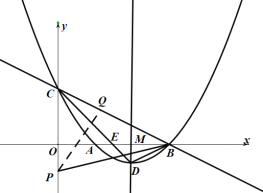
同理可得![]() .
.
设![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,
解得![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
综上所述,点P的坐标为![]() 或
或![]() .
.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】2019新型冠状病毒,因武汉病毒性肺炎病例而被发现,2020年1月12日被世界卫生组织命名“2019-nCoV”.冠状病毒是一个大型病毒家族,借助电子显微镜,我们可以看到这些病毒直径约为125纳米(1纳米=1 ![]() 10-9米),125纳米用科学记数法表示等于( )米
10-9米),125纳米用科学记数法表示等于( )米
A.1.25![]() 10-10B.1.25
10-10B.1.25![]() 10-11C.1.25
10-11C.1.25 ![]() 10-8D.1.25
10-8D.1.25![]() 10-7
10-7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】服装专卖店计划购进A,B两种型号的精品女装.已知3件A型女装和2件B型女装共需5400元;2件A型女装和1件B型女装共需3200元.
(1)求A,B两种型号女装的单价;
(2)专卖店购进A,B两种型号的女装共60件,其中A型的件数不少于B型件数的2倍,如果B型打八折,那么该专卖店至少需要准备多少货款.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学艺术节期间,向学校学生征集书画作品.九年级美术李老师从全年级14个班中随机抽取了A、B、C、D四个班,对征集到的作品的数量进行了分析统计,制作了如下两幅不完整的统计图.
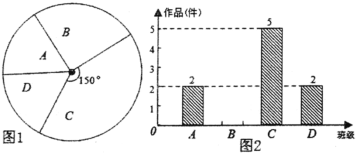
(1)李老师采取的调查方式是______________(填“普查”或“抽样调查”),李老师所调查的4个班征集到作品共_________件,其中B班征集到作品_______________件.
(2)如果全年级参展作品中有4件获得一等奖,其中有2名作者是男生,2名作者是女生.现在要抽取两人去参加学校总结表彰座谈会,求恰好抽中一男一女的概率.(要求用树状图或列表法写出分析过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年,由于“疫情”的原因,学校未能准时开学,某中学为了了解学生在家“课间”活动情况,在七、八、九年级的学生中,分别抽取了相同数量的学生对“你最喜欢的运动项目”在线进行调查(每人只能选一项),调查结果的部分数据如下表(图)所示,其中七年级最喜欢跳绳的人数比八年级多5人,九年级最喜欢排球的人数为10人.
七年级学生最喜欢的运动项目人数统计表
项目 | 排球 | 篮球 | 踢毽 | 跳绳 | 其他 |
人数(人) | 7 | 8 | 14 | 6 |
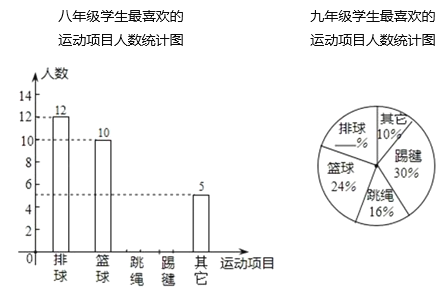
请根据以上统计表(图)解答下列问题:
(1)本次调查共抽取的人数为 人;
(2)请直接补全统计表和统计图;
(3)根据抽样调查的结果,请你估计该校1500名学生中有多少名学生最喜欢踢毽子?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展以“学习朱子文化,弘扬理学思想”为主题的读书月活动,并向学生征集读后感,学校将收到的读后感篇数按年级进行统计,绘制了以下两幅统计图(不完整).
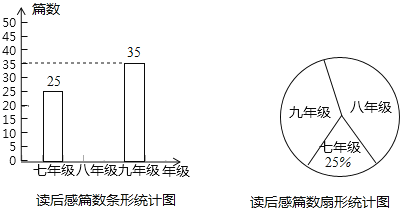
据图中提供的信息完成以下问题
(1)扇形统计图中“八年级”对应的圆心角是 °,并补全条形统计图;
(2)经过评审,全校有4篇读后感荣获特等奖,其中有一篇来自七年级,学校准备从特等奖读后感中任选两篇在校广播电台上播出,请利用画树状图或列表的方法求出七年级特等奖读后感被校广播电台播出的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某工艺厂为配合北京奥运,设计了一款成本为20元∕件的工艺品投放市场进行试销.经过调查,得到如下数据:
销售单价x(元/件) | … | 30 | 40 | 50 | 60 | … |
每天销售量y(件) | … | 500 | 400 | 300 | 200 | … |
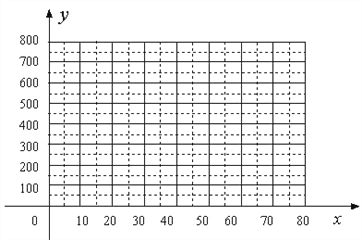
(1)把上表中x、y的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想y与x的函数关系,并求出函数关系式;
(2)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?(利润=销售总价﹣成本总价)
(3)当地物价部门规定,该工艺品销售单价最高不能超过45元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
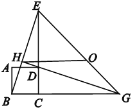
【题目】如图,四边形ABCD是正方形,ΔECG是等腰直角三角形,∠BGE的平分线过点D交BE 于H,O是EG的中点,对于下面四个结论:①GH⊥BE;②OH∥BG,且![]() ;③
;③![]() ;④△EBG的外接圆圆心和它的内切圆圆心都在直线HG上.其中表述正确的个数是( )
;④△EBG的外接圆圆心和它的内切圆圆心都在直线HG上.其中表述正确的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市教育行政部门为了解初中学生参加综合实践活动的情况,随机抽取了本市初一、初二、初三年级各![]() 名学生进行了调查,调查结果如图所示,请你根据图中的信息回答问题.
名学生进行了调查,调查结果如图所示,请你根据图中的信息回答问题.
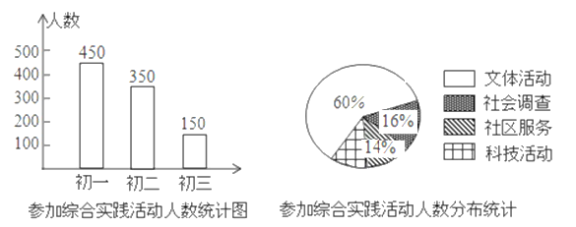
(1)在被调查的学生中,参加综合实践活动的有多少人,参加科技活动的有多少人;
(2)如果本市有![]() 万名初中学生,请你估计参加科技活动的学生约有多少名.
万名初中学生,请你估计参加科技活动的学生约有多少名.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com