
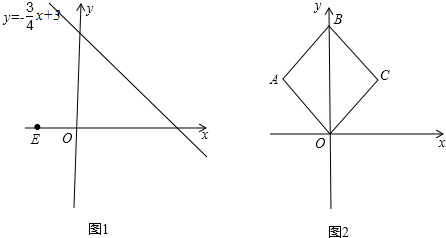
���� ��1���ٸ����Ա����뺯��ֵ�Ķ�Ӧ��ϵ���ɵ�P�����꣬����|x1-x2|+|y1-y2|����A��B����֮���ֱ�Ǿ��룬����d��A��B�����ɵô𰸣�
�ڷ������ۣ�x��-1��x��-1������|x1-x2|+|y1-y2|����A��B����֮���ֱ�Ǿ��룬����d��A��B��
��2�����ݺ�����ϵʽ���ɵ�P��Q������꣬����|x1-x2|+|y1-y2|����A��B����֮���ֱ�Ǿ��룬����d��P��Q�����ɵô𰸣�
��� �⣺��1��������P������Ϊ��l��t������P��1��$\frac{9}{4}$����
��d��O��P��=|1-0|+|$\frac{9}{4}$-0|=1+$\frac{9}{4}$=$\frac{13}{4}$��
�ʴ�Ϊ��$\frac{13}{4}$��
�ڵ�x��-1ʱ��d��P��E��=|x+1|+|-$\frac{3}{4}$x+3|=x+1-$\frac{3}{4}$x+3=$\frac{1}{4}$x+4��
x=-1ʱ��d��P��E����С=$\frac{15}{4}$��
��x��-1ʱ��d��P��E��=|x+1|+|-$\frac{3}{4}$x+3|=-x-1-$\frac{3}{4}$x+3=-$\frac{7}{4}$x+2��
x=-1ʱ��d��P��E����С=$\frac{15}{4}$��
��������d��P��E����С=$\frac{15}{4}$��
��2��BC�Ľ���ʽΪy=-x+2��
��Q��x��-x+2����P��x��kx+b����
d��P��Q����С=|x-x|+|kx+b+x-2|=��k+1��x+b-2��
��-1��k��0ʱ��x=0ʱ��d��P��Q����С=b-2��
��k=-1ʱ��d��P��Q����С=b-2��
��k��-1ʱ��x=1ʱ��d��P��Q����С=k+b-1��
����������d��P��Q����С=$\left\{\begin{array}{l}{b-2��-1��k��0��}\\{k+b-1��k��-1��}\end{array}\right.$��
���� ���⿼����һ�κ����ۺ��⣬������ֱ�Ǿ��룬���������ǽ���ؼ����Է���©��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
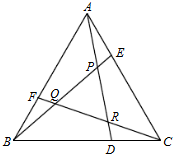 ��ͼ��ʾ����֪��ABC���Ϊl����D��E��F�ֱ���BC��CA��AB�ϣ���BD=2DC��CE=2EA��AF=2FB��AD��BE��CF�����ཻ��P��Q��R�����PQR�����Ϊ��������
��ͼ��ʾ����֪��ABC���Ϊl����D��E��F�ֱ���BC��CA��AB�ϣ���BD=2DC��CE=2EA��AF=2FB��AD��BE��CF�����ཻ��P��Q��R�����PQR�����Ϊ��������| A�� | $\frac{1}{5}$ | B�� | $\frac{1}{6}$ | C�� | $\frac{1}{7}$ | D�� | $\frac{1}{14}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
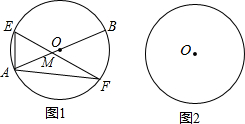 ��֪ABΪ��O��ֱ������EF���ڵ�ֱ����ֱ��AB���ڵ�M
��֪ABΪ��O��ֱ������EF���ڵ�ֱ����ֱ��AB���ڵ�M�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com