
【题目】如图,Rt△ABC纸片中,∠C=90°,AC=3,BC=4,点D在边BC上,以AD为折痕将△ABD折叠得到△AB’D,AB'与边BC交于点E.若△DEB’为直角三角形,则BD的长是________.

【答案】1或![]()
【解析】
由勾股定理可求出AB,若△DEB′为直角三角形,则有(1)∠EDB′=90°,(2)∠DEB′=90°两种情况,因此分别画出图形,在第(1)种情况中,由折叠和三角形的内角和可证△ACE∽△BCA,求出CE、AE的长,进而求出DE、EB′,在Rt△DEB′中,设未知数,列方程求解即可,在第(2)种情况中,点E与点C重合,求出EB′,在Rt△DEB′中,由勾股定理列方程求解即可.
解:在Rt△ACB中,
∵ ∠C=90°,AC=3,BC=4,
∴AB=5,
又∵ 以AD为折痕将△ABD折叠得到△ABD,
∴BD=BD,AB=AB=5,
∵△DEB为直角三角形,
∴①如图1所示:当∠BDE=90°时,过B作BF⊥AC交AC延长线于F,

设BD=BD=x,
∴AF=AC+CF=3+x,BF=CD=CB-BD=4-x,
在Rt△AFB中,
∴AF2+BF2=AB2 ,
即(3+x)2+(4-x)2=52 ,
解得:x=1或x=0(舍去),
∴BD=BD=1,
②如图2所示:当∠BED=90°时,此时点C与点E重合,

∵AB=5,AC=3,
∴BE=AB-AC=5-3=2,
设BD=BD=y,
∴CD=BC-BD=4-y,
在Rt△BDE中,
∴BE2+DE2=DB2 ,
即(4-y)2+22=y2 ,
解得:y=![]() ,
,
∴BD=BD=![]() ,
,
综上所述:BD的长为1或![]() .
.
故答案为:1或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DCB中,∠BAC=∠CDB=90°,AB=DC,AC与BD交于点O.
(1)求证:△ABC≌△DCB.
(2)当∠DBC=30°,BC=6时,求BO的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,长方形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2, 0)同时出发,沿长方形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位长度秒匀速运动,物体乙按顺时针方向以2个单位长度秒匀速运动,则两个物体运动后的第2020次相遇点的坐标是( )

A.(2,0)B.(-1,-1)C.( -2,1)D.(-1, 1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列要求,解答相关问题.
(1)请补全以下求不等式﹣2x2﹣4x≥0的解集的过程
①构造函数,画出图象:根据不等式特征构造二次函数y=﹣2x2﹣4x;并在下面的坐标系中(图1)画出二次函数y=﹣2x2﹣4x的图象(只画出图象即可).
②求得界点,标示所需,当y=0时,求得方程﹣2x2﹣4x=0的解为______;并用锯齿线标示出函数y=﹣2x2﹣4x图象中y>0的部分.
③借助图象,写出解集:由所标示图象,可得不等式﹣2x2﹣4x>0的解集为_______.
(2)利用(1)中求不等式解集的步骤,求不等式x2﹣2x+1≥4的解集.
①构造界点,画出图象;
②求得界点,标志所需;
③借助图象,写出解集


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点E,F分别平行四边形ABCD是的边BC,AD上的点,点E是线段BC的中点,且AE=BE,CF=FD,tanB=![]() ,若CD=4,求四边形AECF的周长.
,若CD=4,求四边形AECF的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
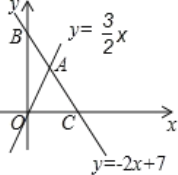
【题目】如图,直线y=﹣2x+7与x轴、y轴分别相交于点C、B,与直线y=![]() x相交于点A.
x相交于点A.
(1)求A点坐标;
(2)求△OAC的面积;
(3)如果在y轴上存在一点P,使△OAP是以OA为底边的等腰三角形,求P点坐标;
(4)在直线y=﹣2x+7上是否存在点Q,使△OAQ的面积等于6?若存在,请求出Q点的坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com