
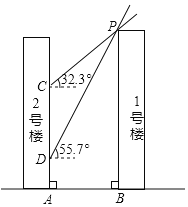
【题目】如图,1号楼在2号楼的南侧,楼间距为AB.冬至日正午,太阳光线与水平面所成的角为32.3°,1号楼在2号楼墙面上的影高为CA;春分日正午,太阳光线与水平面所成的角为55.7°,1号楼在2号楼墙面上的影高为DA.已知CD=35m.请求出两楼之间的距离AB的长度(结果保留整数)
(参考数据:sin32.3°≈0.53,cos32.3°≈0.85,tan32.3°≈0.63,sin55.7°≈0.83,cos55.7°≈0.56,tan55.7°≈1.47)
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
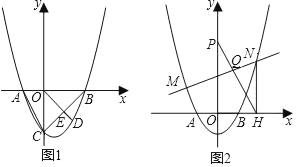
【题目】如图1,抛物线y=x2+(m﹣2)x﹣2m(m>0)与x轴交于A、B两点(A在B左边),与y轴交于点C.连接AC、BC,D为抛物线上一动点(D在B、C两点之间),OD交BC于E点.
(1)若△ABC的面积为8,求m的值;
(2)在(1)的条件下,求![]() 的最大值;
的最大值;
(3)如图2,直线y=kx+b与抛物线交于M、N两点(M不与A重合,M在N左边),连MA,作NH⊥x轴于H,过点H作HP∥MA交y轴于点P,PH交MN于点Q,求点Q的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
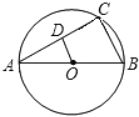
【题目】如图,已知AB为⊙O的直径,AC为弦,OD∥BC,交AC于D,BC=4cm.
(1)求证:AC⊥OD;
(2)求OD的长;
(3)若2sinA﹣1=0,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
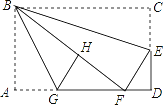
【题目】如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,①∠EBG=45°;②△DEF∽△ABG;③S△ABG=![]() S△FGH;④AG+DF=FG.则下列结论正确的有( )
S△FGH;④AG+DF=FG.则下列结论正确的有( )
A. ①②④ B. ①③④ C. ②③④ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
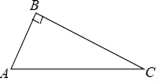
【题目】如图,已知△ABC中,∠ABC=90°.
(1)尺规作图:按下列要求完成作图(保留作图痕迹,请标明字母)
①作线段AC的垂直平分线l,交AC于点O;
②连接BO并延长,在BO的延长线上截取OD,使得OD=OB;
③连接DA、DC.
(2)试判断AD、CD的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
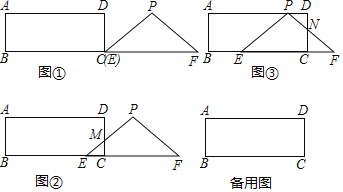
【题目】已知:Rt△EFP和矩形ABCD如图①摆放(点C与点E重合),点B,C(E),F在同一直线上,AB=3cm,BC=9cm,EF=8cm,PE=PF=5cm,如图②,△EFP从图①的位置出发,沿CB方向匀速运动,速度为2cm/s,当点F与点C重合时△EFP停止运动停止.设运动时间为t(s)(0<t<4),解答下列问题:
(1)当0<t<2时,EP与CD交于点M,请用含t的代数式表示CE=______,CM=______;
(2)当2<t<4时,如图③,PF与CD交于点N,设四边形EPNC的面积为y(cm2),求y与t之间的函数关系式;
(3)当2<t<4时,且S四边形EPNC:S矩形ABCD=1:4时,请求出t的值;
(4)连接BD,在运动过程中,当BD与EP相交时,设交点为O,当t=______时;O在∠BAD的平分线上.(不需要写解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
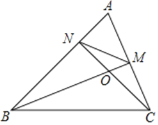
【题目】如图,△ABC中,∠A=60°,BM⊥AC于点M,CN⊥AB于点N,BM,CN交于点O,连接MN.下列结论:①∠AMN=∠ABC;②图中共有8对相似三角形;③BC=2MN.其中正确的个数是( )
A. 1个B. 2个C. 3个D. 0个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=![]() x2-mx+
x2-mx+![]() m2-2(m为大于0的常数)与x轴交于A,B两点(点A在点B的左侧)
m2-2(m为大于0的常数)与x轴交于A,B两点(点A在点B的左侧)
(1)若点A的坐标为(1,0)
①求抛物线的表达式;
②当n≤x≤2时,函数值y的取值范围是-![]() ≤y≤5-n,求n的值;
≤y≤5-n,求n的值;
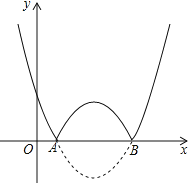
(2)将抛物线在x轴下方的部分沿x轴翻折,得到新的函数的图象,如图,当2<x<3时,若此函数的值随x的增大而减小,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:

(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入-成本);
(3)试说明(2)中总利润W随售价x的变化而变化的情况,并指出售价为多少元时获得最大利润,最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com