
【题目】如图,Rt△ABC中,∠ABC=90°,点D,F分别是AC,AB的中点,CE∥DB,BE∥DC,AD=3,DF=1,四边形DBEC面积是_____

【答案】4![]()
【解析】
根据平行四边形的判定定理首先推知四边形DBEC为平行四边形,然后由直角三角形斜边上的中线等于斜边的一半得到其邻边相等:CD=BD,得出四边形DBEC是菱形,由三角形中位线定理和勾股定理求得AB边的长度,然后根据菱形的性质和三角形的面积公式进行解答.
∵CE∥DB,BE∥DC,
∴四边形DBEC为平行四边形.
又∵Rt△ABC中,∠ABC=90°,点D是AC的中点,
∴CD=BD=![]() AC,
AC,
∴平行四边形DBEC是菱形;
∵点D,F分别是AC,AB的中点,AD=3,DF=1,
∴DF是△ABC的中位线,AC=2AD=6,S△BCD=![]() S△ABC,
S△ABC,
∴BC=2DF=2.
又∵∠ABC=90°,
∴AB=![]() =
=![]() .
.
∵平行四边形DBEC是菱形,
∴S四边形DBEC=2S△BCD=S△ABC=![]() ABBC=
ABBC=![]() ×4
×4![]() ×2=4
×2=4![]() ,
,
故答案为:4![]() .
.


科目:初中数学 来源: 题型:
【题目】某次考试中,某班级的数学成绩统计图如下.下列说法错误的是( )

A. 得分在70~80分之间的人数最多
B. 该班的总人数为40
C. 得分在90~100分之间的人数最少
D. 及格(≥60分)人数是26
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=90°,点A,B分别在射线OM,ON上移动,∠OAB的平分线与∠OBA的外角平分线交于点C,试猜想:随着点A,B的移动,∠ACB的大小是否发生变化,并说明理由.
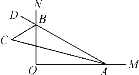
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某华为手机专卖店销售5台甲型手机和8台乙型手机的利润为1600元,销售15台甲型手机和6台乙型手机的利润为3000元
(1) 求每台甲型手机和乙型手机的利润
(2) 专卖店计划购进两种型号的华为手机共120台,其中乙型手机的进货量不低于甲型手机的2倍.设购进甲型手机x台,这120台手机全部销售的销售总利润为y元
① 直接写出y关于x的函数关系式_______________,x的取值范围是_______________
② 该商店如何进货才能使销售总利润最大?说明原因
(3) 专卖店预算员按照(2)中的方案准备进货,同时专卖店对甲型手机销售价格下调a元,结果预算员发现无论按照哪种进货方案最后销售总利润不变.请你判断有这种可能性吗?如果有,求出a的值;如果没有,说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题
情景:

试根据图中的信息,解答下列问题:
(1)购买6根跳绳需___________元,购买12根跳绳需_____________元.
(2)小红比小明多买2根,付款时小红反而比小明少5元,你认为有这种可能吗?若有,请求出小红购买跳绳的根数;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD对角线交于点O,BE∥AC,AE∥BD,EO与AB交于点F.
(1)试判断四边形AEBO的形状,并说明你的理由;
(2)求证:EO=DC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】光华农机租赁公司共有50台联合收割机,其中甲型20台,乙型30台,先将这50台联合收割机派往A、B两地区收割小麦,其中30台派往A地区,20台派往B地区.两地区与该农机租赁公司商定的每天的租赁价格见表:
每台甲型收割机的租金 | 每台乙型收割机的租金 | |
A地区 | 1800 | 1600 |
B地区 | 1600 | 1200 |
(1)设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y(元),求y与x间的函数关系式,并写出x的取值范围;
(2)若使农机租赁公司这50台联合收割机一天获得的租金总额不低于79 600元,说明有多少种分配方案,并将各种方案设计出来;
(3)如果要使这50台联合收割机每天获得的租金最高,请你为光华农机租赁公司提一条合理化建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场服装部分为了解服装的销售情况,统计了每位营业员在某月的销售额(单位:万元),并根据统计的这组销售额的数据,绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
该商场服装营业员的人数为 ,图①中m的值为 ;
求统计的这组销售额数据的平均数、众数和中位数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=3,AD=4,动点Q从点A出发,以每秒1个单位的速度,沿AB向点B移动;同时点P从点B出发,仍以每秒1个单位的速度,沿BC向点C移动,连接QP,QD,PD.若两个点同时运动的时间为x秒(0<x≤3),解答下列问题: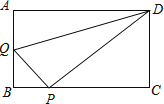
(1)设△QPD的面积为S,用含x的函数关系式表示S;当x为何值时,S有最大值?并求出最小值;
(2)是否存在x的值,使得QP⊥DP?试说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com