
【题目】如图,菱形ABCD对角线交于点O,BE∥AC,AE∥BD,EO与AB交于点F.
(1)试判断四边形AEBO的形状,并说明你的理由;
(2)求证:EO=DC.

科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AD>AB. 
(1)作出∠ABC的平分线(尺规作图,保留作图痕迹,不写作法);
(2)若(1)中所作的角平分线交AD于点E,AF⊥BE,垂足为点O,交BC于点F,连接EF.求证:四边形ABFE为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 已知:如图
已知:如图![]() ,易知
,易知![]() P
P![]() ,请补充完整证明过程:
,请补充完整证明过程:
证明:过点P作![]()
![]() 已作
已作![]()
![]() ______
______![]() ______
______![]() ,
,
又![]()
![]() ______
______![]() ______
______![]()
即![]()
![]() 变式:
变式:
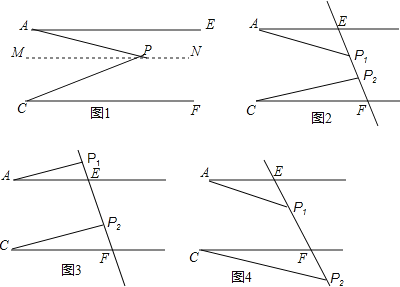
如图![]() 是直线EF上的两点,猜想
是直线EF上的两点,猜想![]()
![]()
![]()
![]() 这四个角之间的关系,并直接写出以下三种情况下这四个角之间的关系.
这四个角之间的关系,并直接写出以下三种情况下这四个角之间的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ABC=90°,点D,F分别是AC,AB的中点,CE∥DB,BE∥DC,AD=3,DF=1,四边形DBEC面积是_____

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是正方形,AC与BD,相交于点O,点E、F是直线AD上两动点,且AE=DF,CF所在直线与对角线BD所在直线交于点G,连接AG,直线AG交BE于点H.

(1)如图1,当点E、F在线段AD上时,求证:∠DAG=∠DCG;
(2)如图1,猜想AG与BE的位置关系,并加以证明;
(3)如图2,在(2)条件下,连接HO,试说明HO平分∠BHG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平安路与幸福路是两条平行的道路,且都与新兴大街垂直,老街与小米胡同垂直,书店位于老街与小米胡同的交口处.如果小强同学站在平安路与新兴大街交叉路口,准备去书店,按图中的街道行走,最近的路程为( )

A. 300m B. 400m C. 500m D. 700m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△AOB的顶点O为坐标原点,点A的坐标为(4,0),点B的坐标为(0,1),点C为边AB的中点,正方形OBDE的顶点E在x轴的正半轴上,连接CO,CD,CE.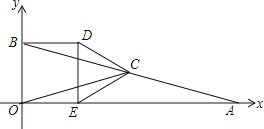
(1)线段OC的长为;
(2)求证:△CBD≌△COE;
(3)将正方形OBDE沿x轴正方向平移得到正方形O1B1D1E1 , 其中点O,B,D,E的对应点分别为点O1 , B1 , D1 , E1 , 连接CD,CE,设点E的坐标为(a,0),其中a≠2,△CD1E1的面积为S.
①当1<a<2时,请直接写出S与a之间的函数表达式;
②在平移过程中,当S= ![]() 时,请直接写出a的值.
时,请直接写出a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售国外、国内两种品牌的智能手机,这两种手机的进价和售价如表所示
国外品牌 | 国内品牌 | |
进价(万元/部) | 0.44 | 0.2 |
售价(万元/部) | 0.5 | 0.25 |
该商场计划购进两种手机若干部,共需14.8万元,预计全部销售后可获毛利润共2.7万元.[毛利润=(售价﹣进价)×销售量]
(1)该商场计划购进国外品牌、国内品牌两种手机各多少部?
(2)通过市场调研,该商场决定在原计划的基础上,减少国外品牌手机的购进数量,增加国内品牌手机的购进数量.已知国内品牌手机增加的数量是国外品牌手机减少的数量的3倍,而且用于购进这两种手机的总资金不超过15.6万元,该商场应该怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com