
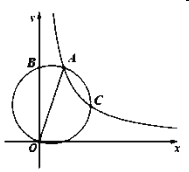
【题目】如图,点![]() 在反比例函数
在反比例函数![]() 上,以线段
上,以线段![]() 为直径的圆交该双曲线于点
为直径的圆交该双曲线于点![]() ,交
,交![]() 轴于点
轴于点![]() ,若弧
,若弧![]() 弧
弧![]() ,则点
,则点![]() 的坐标为( )
的坐标为( )
A.![]() B.
B.![]() C.
C.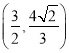 D.
D.![]()
【答案】B
【解析】
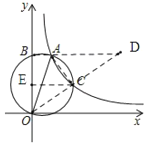
连接OC并延长OC,BA交点为D,作CE⊥OB,连接AC,设A(a,b) 则ab=2![]() ,AO=
,AO=![]() .由AO为直径可证得∠BOC=∠CAD,由
.由AO为直径可证得∠BOC=∠CAD,由![]() 可得∠BOC=∠OAC则∠OAC=∠DAC,可证△AOC≌△ACD,所以AO=AD,OC=CD,由垂径定理得BE=OE=
可得∠BOC=∠OAC则∠OAC=∠DAC,可证△AOC≌△ACD,所以AO=AD,OC=CD,由垂径定理得BE=OE=![]() ,由中位线定理可得EC=
,由中位线定理可得EC=![]() BD,最后由S△ABO=S△ECO,用a,b表示面积,可得a,b 的关系式,代入ab=2
BD,最后由S△ABO=S△ECO,用a,b表示面积,可得a,b 的关系式,代入ab=2![]() ,可得a,b的值.
,可得a,b的值.
如图:连接OC并延长OC,BA交点为D,作CE⊥OB,连接AC
设A(a,b) 则ab=2![]()
∵AB是直径
∴∠ABO=90°=∠ACO
∴AB=a,OB=b
∴AO=![]()
∵ABOC是圆的内接四边形
∴∠BOC=∠DAC
∵![]()
∴∠BOC=∠OAC
∴∠OAC=∠DAC,且AC=AC,∠ACO=∠ACD=90°
∴△AOC≌△ACD
∴AO=AD=![]() ,OC=CD
,OC=CD
∵CE⊥OB,![]()
∴OE=BE=![]() ,且OC=CD
,且OC=CD
∴EC∥BD,EC=![]() BD=
BD=![]()
∵S△ABO=S△EOC=![]()
∴![]() ab=
ab=![]() ×
×![]() ×(
×(![]() )
)
解得3a=![]()
∴b=2![]() 且ab=2
且ab=2![]()
∴a=1,b=2![]()
∴A![]() ,
,
故选B.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】观察下列一组方程:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;…
;…
它们的根有一定的规律,都是两个连续的自然数,我们称这类一元二次方程为“连根一元二次方程”。若![]() 也是“连根一元二次方程”,则
也是“连根一元二次方程”,则![]() 的值为________,第
的值为________,第![]() 个方程为______________.
个方程为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实视力保护工作,某校组织七年级学生开展了视力保健活动.活动前随机测查了30名学生的视力,活动后再次测查这部分学生的视力.两次相关数据记录如下:
活动前被测查学生视力数据:
4.0,4.1,4.1,4.2,4.2,4.3,4.3,4.4,4.4,4.4,4.5,4.5,4.6,4.6,4.6
4.7,4.7,4.7,4.7,4.8,4.8,4.8,4.8,4.8,4.9,4.9,4.9,5.0,5.0,5.1
活动后被测查学生视力数据:
4.0,4.2,4.3,4.4,4.4,4.5,4.5,4.6,4.6,4.6,4.7,4.7,4.7,4.7,4.8
4.8,4.8,4.8,4.8,4.8,4.8,4.9,4.9,4.9,4.9,4.9,5.0,5.0,5.1,5.1
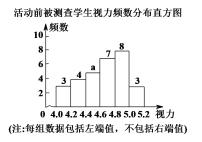

根据以上信息回答下列问题:
(1)填空:a= ,b= ,活动前被测查学生视力样本数据的中位数是 ,活动后被测查学生视力样本数据的众数是 ;
(2)若视力在4.8及以上为达标,估计七年级600名学生活动后视力达标的人数有多少?
(3)分析活动前后相关数据,从一个方面评价学校开展视力保健活动的效果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业安排65名工人生产甲、乙两种产品,每人每天生产2件甲或1件乙,甲产品每件可获利15元。根据市场需求,乙产品每天产量不少于5件,当每天生产5件时,每件可获利120元,每增加1件,当天平均每件利润减少2元,设每天安排![]() 人生产乙产品。
人生产乙产品。
(1)根据信息填表:
产品种类 | 每天工人数(人) | 每天产量(件) | 每件产品可获利润(元) |
甲 | — | — | 15 |
乙 |
|
| — |
(2)该企业在不增加工人的情况下,增加生产丙产品,要求每天甲、丙两种产品的产量相等,已知每人每天可生产1件丙(每人每天只能生产一件产品),丙产品每件可获利30元,求每天生产三种产品可获得的总利润![]() (元)的最大值及相应的
(元)的最大值及相应的![]() 值。
值。
查看答案和解析>>
科目:初中数学 来源: 题型:
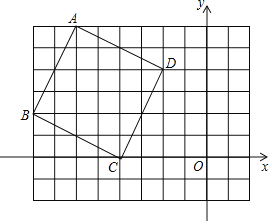
【题目】如图,在平面直角坐标系中,四边形ABCD的坐标分别为A(﹣6,6),B(﹣8,2),C(﹣4,0),D(﹣2,4).
(1)画出一个四边形A′B′C′D′,使四边形A′B′C′D′与四边形ABCD是以原点O为位似中心,相似比为1:2的位似图形.
(2)直接写出点的坐标:A′( ),B′( ),C′( ),D′( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 的顶点
的顶点![]() 在反比例函数
在反比例函数![]() 的图象上,且
的图象上,且![]() ,
,![]() .若动点
.若动点![]() 从
从![]() 开始沿
开始沿![]() 向
向![]() 以每秒1个单位长度的速度运动,同时动点
以每秒1个单位长度的速度运动,同时动点![]() 从
从![]() 开始沿
开始沿![]() 向
向![]() 以每秒2个单位长度的速度运动,当其中一个动点到达端点时,另一个动点随之停止运动,设运动时间为
以每秒2个单位长度的速度运动,当其中一个动点到达端点时,另一个动点随之停止运动,设运动时间为![]() 秒.
秒.
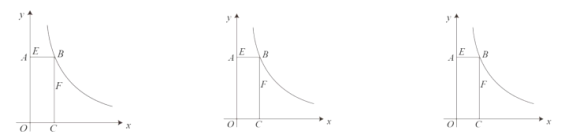
(1)求反比例函数的表达式;
(2)当![]() 时,在
时,在![]() 轴上存在点
轴上存在点![]() ,使
,使![]() 的周长最小,请求出此时点
的周长最小,请求出此时点![]() 的坐标,并直接写出
的坐标,并直接写出![]() 的周长最小值;
的周长最小值;
(3)在双曲线上是否存在一点![]() ,使以点
,使以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形?若存在,请直接写出满足条件
为顶点的四边形是平行四边形?若存在,请直接写出满足条件![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
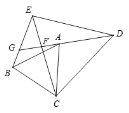
【题目】如图,已知△ABC和△DCE是等边三角形,连接BE,连接DA并延长交CE于点F,交BE于点G,CD=6,EF=2,那么EG的长为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com