
【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O且AC、BD的长(![]() )是方程
)是方程![]() 的两个根.点P从点A出发,以每秒1个单位的速度沿
的两个根.点P从点A出发,以每秒1个单位的速度沿![]() 边A→O→B→A的方向运动,运动时间为t(秒).
边A→O→B→A的方向运动,运动时间为t(秒).

(1)求AC和BD的长;
(2)求当AP恰好平分![]() 时,点P运动时间t的值;
时,点P运动时间t的值;
(3)在运动过程中,是否存在点P,使![]() 是等腰三角形?若存在,请求出运动时间t的值:若不存在,请说明理由.
是等腰三角形?若存在,请求出运动时间t的值:若不存在,请说明理由.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 秒;(3)存在,综上:
秒;(3)存在,综上:![]() 18秒或16.8秒或12秒或
18秒或16.8秒或12秒或![]() .
.
【解析】
(1)解方程![]() 得两根为12和16,所以
得两根为12和16,所以![]() ,
,![]() ;
;
(2)设点![]() 运动
运动![]() 秒时,
秒时,![]() 平分
平分![]() ,如图,过点P作
,如图,过点P作![]() 于Q,利用角平分线定理把已知和未知线段都归结到直角
于Q,利用角平分线定理把已知和未知线段都归结到直角![]() 中,利用勾股定理构造方程,可求得
中,利用勾股定理构造方程,可求得![]() 的值;
的值;
(3)分别以AO为腰,A为顶点;AO为腰,O为顶点;AO为底构造等腰三角形,画图,通过计算可求得答案.
(1)方程![]() 可化成
可化成![]()
∴![]()
∵![]()
故![]() ,
,![]() ;
;
(2)设点![]() 运动
运动![]() 秒时,
秒时,![]() 平分
平分![]() ,
,
如图,过点P作![]() 于Q,
于Q,
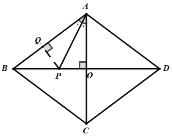
∵![]() ,
,![]() ,四边形ABCD是菱形,
,四边形ABCD是菱形,
∴![]() ,
,![]() ,
,
在直角![]() 中,∵
中,∵![]() ,
,![]() ,∴
,∴![]() ;
;
∵![]() 平分
平分![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
![]() ,
,
![]() ,
,
![]() 为直角三角形,
为直角三角形,![]()
即:![]() ,化简并求得:
,化简并求得:![]() .
.
故答案是:![]() 秒.
秒.
(3)存在.
以![]() 为腰,
为腰,![]() 为顶点的等腰三角形,如图:
为顶点的等腰三角形,如图:
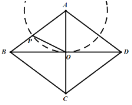
∵![]()
∴![]() ;
;
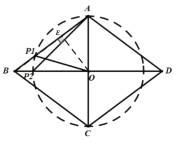
以![]() 为腰,
为腰,![]() 为顶点的等腰三角形,如图:
为顶点的等腰三角形,如图:
作![]() 于E,
于E,
在Rt![]() 和Rt
和Rt![]() 中:
中:
![]() 公共,∴Rt
公共,∴Rt![]() Rt
Rt![]()
![]() ,即
,即![]() ,∴
,∴![]() ,
,
∵![]() , ∴
, ∴![]()
∴![]() ;
;
∵![]() ,
,
∴![]() ;
;
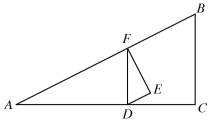
以AO为底的等腰三角形,如图:
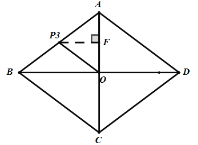
过![]() 作
作![]() 于
于![]() ,
,
![]() ,∴点F为AO中点,
,∴点F为AO中点,
![]() 四边形ABCD为菱形,∴
四边形ABCD为菱形,∴![]() ,
,
又![]() ,∴
,∴![]() ,
,
![]() 是AB中点,
是AB中点,![]() ,
,
∴![]() ;
;
综上:![]() 18秒或16.8秒或12秒或
18秒或16.8秒或12秒或![]() .
.


科目:初中数学 来源: 题型:
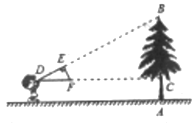
【题目】如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=0.4m,EF=0.2m,测得边DF离地面的高度AC=1.5m,CD=8m,求树高。
查看答案和解析>>
科目:初中数学 来源: 题型:
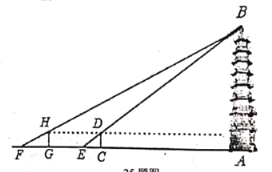
【题目】净觉寺享有“家东第一寺”的美誉,是一座规模较大,布局严颜,结构合理,独具一格的古建筑群体,被国务院批准列入第六批全国重点文物保护单位名单,某校社会实践小组为了测量寺内一古塔的高度,在地面上![]() 处垂直于地面竖立了高度为
处垂直于地面竖立了高度为![]() 米的标杆
米的标杆![]() ,这时地面上的点
,这时地面上的点![]() ,标杆的顶端点
,标杆的顶端点![]() ,古塔的塔尖点
,古塔的塔尖点![]() 正好在同一直线上,测得
正好在同一直线上,测得![]() 米,将标杆向后平移到点处,这时地面上的点
米,将标杆向后平移到点处,这时地面上的点![]() ,标杆的顶端点
,标杆的顶端点![]() ,古塔的塔尖点
,古塔的塔尖点![]() 正好在同一直线上(点
正好在同一直线上(点![]() ,点
,点![]() ,点
,点![]() ,点
,点![]() 与古塔底处的点
与古塔底处的点![]() 在同一直线上)这时测得
在同一直线上)这时测得![]() 米,
米,![]() 米,请你根据以上数据,计算古塔的高度
米,请你根据以上数据,计算古塔的高度![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程(m-1)x2-x-2=0,
(1)若x=-1是方程的一个根,求m的值及另一个根;
(2)当m为何值时方程有两个不同的实数根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,在8×6的网格图中,每个小正方形边长均为1,原点O和△ABC的顶点均为格点.点C坐标为(2,4),以O为位似中心,在网格图中作△ABC,使△A′B′C′与△ABC位似,且位似比为1:2;(保留作图痕迹)
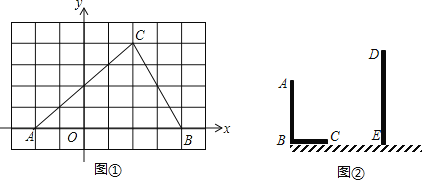
(2)则点C′的坐标为 ,周长比C△A′B′C′:C△ABC= .
(3)如图②,AB和DE是直立在地面上的两根立柱.AB=6m,某一时刻AB在阳光下的投影BC=4m,DE在阳光下的投影长为6m.
①请你在图②中画出此时DE在阳光下的投影EF.
②根据题中信息,求得立柱DE的长为 m.
查看答案和解析>>
科目:初中数学 来源: 题型:
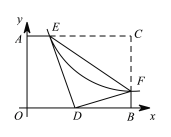
【题目】如图,反比例函数y=![]() (k>0)的图像与矩形AOBC的边AC,BC分别交于点E、F,点C的坐标为(8,6),将△CEF沿EF翻折,C点恰好落在OB上的点D处,则k的值为( )
(k>0)的图像与矩形AOBC的边AC,BC分别交于点E、F,点C的坐标为(8,6),将△CEF沿EF翻折,C点恰好落在OB上的点D处,则k的值为( )
A.![]() B.6C.12D.
B.6C.12D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,直线y=-![]() x+3与x轴相交于点A,与y轴相交于点B,点C(m,n)是第二象限内一点,以点C为圆心的圆与x轴相切于点E,与直线AB相切于点F.
x+3与x轴相交于点A,与y轴相交于点B,点C(m,n)是第二象限内一点,以点C为圆心的圆与x轴相切于点E,与直线AB相切于点F.
(1)当四边形OBCE是矩形时,求点C的坐标;
(2)如图②,若⊙C与y轴相切于点D,求⊙C的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,![]() 中,
中,![]() ,动点
,动点![]() 从
从![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度向终点
个单位长度的速度向终点![]() 运动,过点
运动,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的平行线,与过点
的平行线,与过点![]() 且与
且与![]() 垂直的直线交于点
垂直的直线交于点![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() (秒)
(秒)![]()
(1)用含![]() 的代数式表示线段
的代数式表示线段![]() 的长;
的长;
(2)求当点![]() 落在
落在![]() 边上时t的值;
边上时t的值;
(3)设![]() 与
与![]() 重合部分图形的面积为
重合部分图形的面积为![]() (平方单位),求
(平方单位),求![]() 与的
与的![]() 函数关系式;
函数关系式;
(4)连结![]() ,若将
,若将![]() 沿它自身的某边翻折,翻折前后的两个三角形形成菱形,直接写出此时
沿它自身的某边翻折,翻折前后的两个三角形形成菱形,直接写出此时![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com