练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

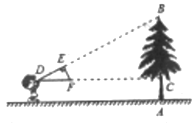
    【题目】如图，小明同学用自制的直角三角形纸板DEF测量树的高度AB，他调整自己的位置，设法使斜边DF保持水平，并且边DE与点B在同一直线上，已知纸板的两条直角边DE=0.4m，EF=0.2m，测得边DF离地面的高度AC=1.5m，CD=8m，求树高。

    【答案】树高为 5.5 米

    【解析】

    根据两角相等的两个三角形相似，可得 △DEF∽△DCB ，利用相似三角形的对边成比例，可得， 代入数据计算即得BC的长，由 AB＝AC+BC ，即可求出树高.

    ∵∠DEF＝∠DCB＝90°，∠D＝∠D，

    ∴△DEF∽△DCB

    ∴ ，

    ∵DE＝0.4m，EF＝0.2m，CD＝8m，

    ∴，

    ∴CB＝4（m），

    ∴AB＝AC+BC＝1.5+4＝5.5（米）

    答：树高为 5.5 米.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

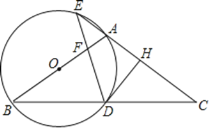
    【题目】如图，在△ABC中，AB＝AC，以AB为直径的⊙O分别交BC于点D，交CA的延长线于点E，过点D作DH⊥AC，垂足为点H，连接DE，交AB于点F．

    （1）求证：DH是⊙O的切线；

    （2）若⊙O的半径为4，

    ①当AE＝FE时，求 的长（结果保留π）；

    ②当 时，求线段AF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

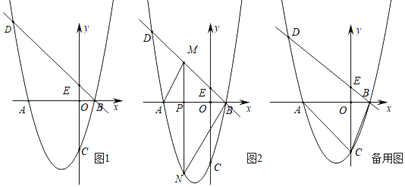
    【题目】如图1，直线1：y＝﹣x+1与x轴、y轴分别交于点B、点E，抛物线L：y＝ax2+bx+c经过点B、点A（﹣3，0）和点C（0，﹣3），并与直线l交于另一点D．

    （1）求抛物线L的解析式；

    （2）点P为x轴上一动点

    ①如图2，过点P作x轴的垂线，与直线1交于点M，与抛物线L交于点N．当点P在点A、点B之间运动时，求四边形AMBN面积的最大值；

    ②连接AD，AC，CP，当∠PCA＝∠ADB时，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

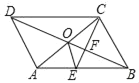
    【题目】如图，ABCD的对角线AC，BD交于点O，CE平分∠BCD交AB于点E，交BD于点F，且∠ABC＝60°，AB＝2BC，连接OE．下列结论：①∠ACD＝30°；②SABCD＝ACBC；③OE：AC＝：6； ④SOEF＝SABCD，成立的是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）如图1，在矩形ABCD中，AB＝2，BC＝5，∠MPN＝90°，且∠MPN的直角顶点在BC边上，BP＝1．

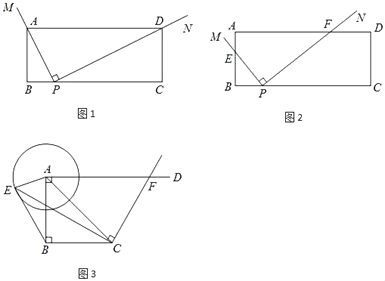
    ①特殊情形：若MP过点A，NP过点D，则＝　 　．

    ②类比探究：如图2，将∠MPN绕点P按逆时针方向旋转，使PM交AB边于点E，PN交AD边于点F，当点E与点B重合时，停止旋转．在旋转过程中，的值是否为定值？若是，请求出该定值；若不是，请说明理由．

    （2）拓展探究：在Rt△ABC中，∠ABC＝90°，AB＝BC＝2，AD⊥AB，⊙A的半径为1，点E是⊙A上一动点，CF⊥CE交AD于点F．请直接写出当△AEB为直角三角形时的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一袋装有编号为1，2，3的三个形状、大小、材质等相同的小球，从袋中随意摸出1个球，记事件A为“摸出的球编号为奇数”，随意抛掷一个之地均匀正方体骰子，六个面上分别写有1﹣6这6个整数，记事件B为“向上一面的数字是3的整数倍”，请你判断等式“P（A）=2P（B）”是否成立，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】费尔兹奖是国际上享有崇高荣誉的一个数学奖项，每4年评选一次，在国际数学家大会上颁给有卓越贡献的年龄不超过40岁的年轻数学家，美籍华人丘成桐1982年获得费尔兹奖．为了让学生了解费尔兹奖得主的年龄情况，我们查取了截止到2018年60名费尔兹奖得主获奖时的年龄数据，并对数据进行整理、描述和分析．下面给出了部分信息．

    a．截止到2018年费尔兹奖得主获奖时的年龄数据的频数分布直方图如图1（数据分成5组，各组是28≤x＜31，31≤x＜34，34≤x＜37，37≤x＜40，x≥40）：

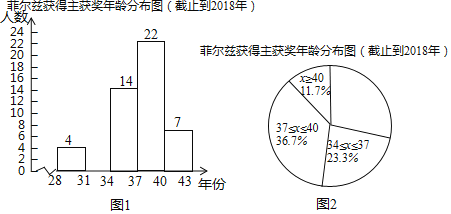
    b．如图2，在a的基础上，画出扇形统计图；

    c．截止到2018年费尔兹奖得主获奖时的年龄在34≤x＜37这一组的数据是：

    36

    35

    34

    35

    35

    34

    34

    35

    36

    36

    36

    36

    34

    35

    d．截止到2018年时费尔兹奖得主获奖时的年龄的平均数、中位数、众数如下：

    年份

    平均数

    中位数

    众数

    截止到2018

    35.58

    m

    37，38

    根据以上信息，回答下列问题：

    （1）依据题意，补全频数直方图；

    （2）31≤x＜34这组的圆心角度数是度，并补全扇形统计图；

    （3）统计表中中位数m的值是；

    （4）根据以上统计图表试描述费尔兹奖得主获奖时的年龄分布特征．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

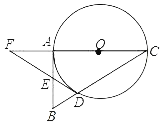
    【题目】如图，在△ABC中，∠BAC＝90°，以AC为直径的⊙O交BC于点D，点E在AB上，连接DE并延长交CA的延长线于点F，且∠AEF＝2∠C．

    （1）判断直线FD与⊙O的位置关系，并说明理由；

    （2）若AE＝2，EF＝4，求⊙O的半径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】发散思维2017·丰台区二模为了解某校八年级学生每周上网的时间，两名学生进行了抽样调查，小丽调查了八年级电脑爱好者中40名学生每周上网的时间，小杰从全校400名八年级学生中随机抽取了40名学生，调查了他们每周上网的时间．小丽与小杰整理各自的样本数据，如下表所示：

    时间段(时/周)

    小丽抽样人数

    小杰抽样人数

    0～1

    6

    22

    1～2

    10

    10

    2～3

    16

    6

    3～4

    8

    2

    (表中每组数据包含最小值，不包含最大值)

    (1)你认为哪名同学抽取的样本不合理？请说明理由；

    (2)专家建议每周上网2小时以上(含2小时)的同学应适当减少上网的时间，估计该校全体八年级学生中有多少名学生应适当减少上网的时间．

    查看答案和解析>>

    同步练习册答案