
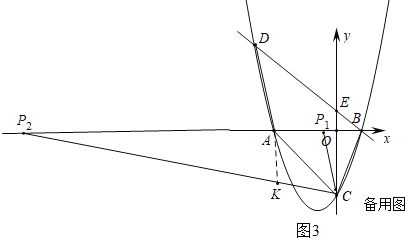
【题目】如图1,直线1:y=﹣x+1与x轴、y轴分别交于点B、点E,抛物线L:y=ax2+bx+c经过点B、点A(﹣3,0)和点C(0,﹣3),并与直线l交于另一点D.
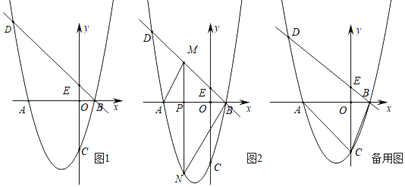
(1)求抛物线L的解析式;
(2)点P为x轴上一动点
①如图2,过点P作x轴的垂线,与直线1交于点M,与抛物线L交于点N.当点P在点A、点B之间运动时,求四边形AMBN面积的最大值;
②连接AD,AC,CP,当∠PCA=∠ADB时,求点P的坐标.
【答案】(1)y=x2+2x﹣3;(2)①S四边形AMBN最大值为![]() ;②P的坐标:P1
;②P的坐标:P1![]() ,P2(﹣15,0).
,P2(﹣15,0).
【解析】
(1)先求出B的坐标,再将A、B、C坐标代入y=ax2+bx+c列方程组,然后求解,即可求出抛物线的解析式;
(2)①根据S四边形AMBN=![]() ABMN=
ABMN=![]() =﹣2(x+
=﹣2(x+![]() )2+
)2+![]() ,所以当x=﹣
,所以当x=﹣![]() 时,S四边形AMBN最大值为
时,S四边形AMBN最大值为![]() ;
;
②先联立方程组.求出D点的坐标,两种情况讨论:Ⅰ.当点P在点A的右边,∠PCA=∠ADB时,△PAC∽△ABD;Ⅱ.当点P在点A的左边,∠PCA=∠ADB时,记此时的点P为P2,则有∠P2CA=∠P1CA.
(1)∵y=﹣x+1,
∴B(1,0),
将A(﹣3,0)、C(0,﹣3),B(1,0)代入y=ax2+bx+c,
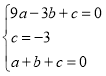 ,
,
∴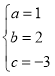
∴抛物线L的解析式:y=x2+2x﹣3;
(2)设P(x,0).
①S四边形AMBN=![]() ABMN
ABMN
=![]()
=﹣2(x+![]() )2+
)2+![]() ,
,
∴当x=﹣![]() 时,S四边形AMBN最大值为
时,S四边形AMBN最大值为![]() ;
;
②由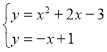 ,得
,得 ,
,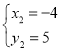 ,
,
∴D(﹣4,5),
∵y=﹣x+1,
∴E(0,1),B(1,0),
∴OB=OE,
∴∠OBD=45°.
∴BD=![]() .
.
∵A(﹣3,0),C(0,﹣3),
∴OA=OC,AC=![]() ,AB=4.
,AB=4.
∴∠OAC=45°,∴∠OBD=∠OAC.
Ⅰ.当点P在点A的右边,∠PCA=∠ADB时,△PAC∽△ABD.
∴![]() ,
,
∴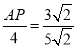 ,
,
∴![]() ,
,
∴P1![]()
Ⅱ.当点P在点A的左边,∠PCA=∠ADB时,记此时的点P为P2,则有∠P2CA=∠P1CA.
过点A作x轴的垂线,交P2C于点K,则∠CAK=∠CAP1,又AC公共边,
∴△CAK≌△CAP1(ASA)
∴AK=AP1=![]() ,
,
∴K(﹣3,﹣![]() ),
),
∴直线CK:![]() ,
,
∴P2(﹣15,0).
P的坐标:P1![]() ,P2(﹣15,0).
,P2(﹣15,0).


科目:初中数学 来源: 题型:
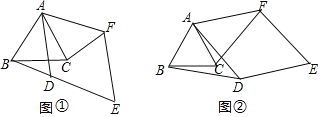
【题目】已知△ABC是等边三角形,四边形ADEF是菱形,∠ADE=120°(AD>AB).
(1)如图①,当AD与边BC相交,点D与点F在直线AC的两侧时,BD与CF的数量关系为___________.
(2)将图①中的菱形ADEF绕点A在平面内逆时针旋转α(0°<α<180°).
Ⅰ.判断(1)中的结论是否仍然成立,请利用图②证明你的结论.
Ⅱ.若AC=4,AD=6,当△ACE为直角三角形时,直接写出CE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 轴,且直线l与抛物线
轴,且直线l与抛物线![]() 和y轴分别交于点A,B,C,点D为抛物线的顶点.若点E的坐标为
和y轴分别交于点A,B,C,点D为抛物线的顶点.若点E的坐标为![]() ,点A的横坐标为1.
,点A的横坐标为1.
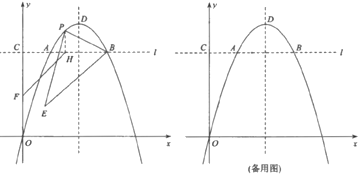
(1)线段AB的长度等于________;
(2)点P为线段AB上方抛物线上的一点,过点P作AB的垂线交AB于点H,点F为y轴上一点,当![]() 的面积最大时,求
的面积最大时,求![]() 的最小值;
的最小值;
(3)在(2)的条件下,删除抛物线![]() 在直线PH左侧部分图象并将右侧部分图象沿直线PH翻折,与抛物线在直线PH右侧部分图象组成新的函数M的图象.现有平行于FH的直线
在直线PH左侧部分图象并将右侧部分图象沿直线PH翻折,与抛物线在直线PH右侧部分图象组成新的函数M的图象.现有平行于FH的直线![]() ,若直线
,若直线![]() 与函数M的图象有且只有2个交点,求t的取值范围(请直接写出t的取值范围,无需解答过程).
与函数M的图象有且只有2个交点,求t的取值范围(请直接写出t的取值范围,无需解答过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(m+2)x+2m=0.
(1)求证:不论m为何值,该方程总有两个实数根;
(2)若直角△ABC的两直角边AB、AC的长是该方程的两个实数根,斜边BC的长为3,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代数学成就的杰出代表作,书中记载:“今有圆材埋壁中,不知大小.以锯锯之,深1寸,锯道长1尺,问经几何?“其意思为:“如图,今有一圆形木材埋在墙壁中,不知其大小用锯子去锯这个木材,锯口深1寸(即DE=1寸),锯道长1尺(即弦AB=1尺),问这块圆形木材的直径是多少?”该问题的答案是_____(注:1尺=10寸)
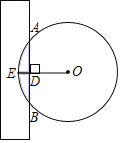
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】民俗村的开发和建设带动了旅游业的发展,某市有A、B、C、D、E五个民俗旅游村及“其它”景点,该市旅游部门绘制了2018年“五一”长假期间民俗村旅游情况统计图如下:
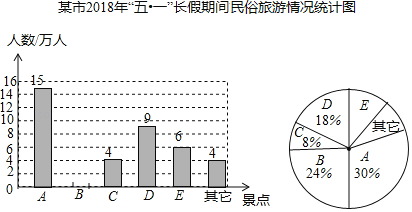
根据以上信息解答:
(1)2018年“五一”期间,该市五个旅游村及“其它”景点共接待游客 万人,扇形统计图中D民俗村所对应的圆心角的度数是 ,并补全条形统计图;
(2)根裾近几年到该市旅游人数增长趋势,预计2019年“五一”节将有70万游客选择该市旅游,请估计有多少万人会选择去E民俗村旅游?
(3)甲、乙两个旅行团在A、C、D三个民俗村中,同时选择去同一个民俗村的概率是多少?请用画树状图或列表法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆某大型车辆企业从去年开始出售“大鼻子安全校车”(以下简称校车).经统计发现,该校车月销售量P(辆)与月份x(1≤x≤12且x取整数)之间的函数关系如下表所示:
月份x | 1 | 2 | 3 | 4 | 5 | … |
月销售量P(辆) | 66 | 68 | 70 | 72 | 74 | … |
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,求出P与x之间的函数关系式;
(2)若该校车在去年上半年的销售价格y1(万元)与月份x之间的函数关系式为y1=﹣0.5x+36(1≤x≤6且x取整数);去年下半年的销售价格y2(万元)与月份x之间的函数关系式为y2=﹣x+39(7≤x≤12且x取整数).此外,已知生产每辆校车的材料成本为12万元,人力和其他成本共4万元.问该企业去年哪个月销售校车的利润最大,并求出这个最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=0.4m,EF=0.2m,测得边DF离地面的高度AC=1.5m,CD=8m,求树高。
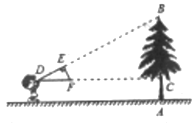
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.
(1)证明与推断:
①求证:四边形CEGF是正方形;
②推断:![]() 的值为 :
的值为 :
(2)探究与证明:
将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG与BE之间的数量关系,并说明理由:
(3)拓展与运用:
正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长CG交AD于点H.若AG=6,GH=2![]() ,则BC= .
,则BC= .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com