
【题目】重庆某大型车辆企业从去年开始出售“大鼻子安全校车”(以下简称校车).经统计发现,该校车月销售量P(辆)与月份x(1≤x≤12且x取整数)之间的函数关系如下表所示:
月份x | 1 | 2 | 3 | 4 | 5 | … |
月销售量P(辆) | 66 | 68 | 70 | 72 | 74 | … |
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,求出P与x之间的函数关系式;
(2)若该校车在去年上半年的销售价格y1(万元)与月份x之间的函数关系式为y1=﹣0.5x+36(1≤x≤6且x取整数);去年下半年的销售价格y2(万元)与月份x之间的函数关系式为y2=﹣x+39(7≤x≤12且x取整数).此外,已知生产每辆校车的材料成本为12万元,人力和其他成本共4万元.问该企业去年哪个月销售校车的利润最大,并求出这个最大利润.
【答案】(1)p=2x+64;(2)该企业去年4月销售校车的利润最大,最大利润为1296万元.
【解析】
(1)观察表格中的数据,可知P与x之间是一次函数关系,设知P与x的函数关系为p=kx+b,由待定系数法即可求解;(1)设1至6月每月的销售利润为W1万元,7至12月每月的销售利润为W2万元,由利润=每辆车的利润×销量,建立W与x的关系式,由抛物线的性质即可解答.
解:(1)设P与x之间的函数关系式为P=kx+b,由题意,得![]()
解得:![]() ,
,
∴P与x之间的函数关系式为:p=2x+64;
(2)设1至6月每月的销售利润为W1万元,7至12月每月的销售利润为W2万元,由题意得,
W1=(2x+64)(﹣0.5x+36﹣12﹣4),
W1=﹣(x﹣4)2+1296,
∴1至6月份,4月销售校车的利润最大,最大利润为1296万元;
W2=(2x+64)(﹣x+39﹣12﹣4),
W2=﹣2(x+4.5)2+1512.5,
∴a=﹣2,抛物线开口向下,对称轴为x=﹣4.5,
∴在对称轴的右侧W2随x的增大而减小,
∴x=7时,W2最大=1248万元.
∵1296>1248,
∴该企业去年4月销售校车的利润最大,最大利润为1296万元.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,某旅游景区为方便游客,修建了一条东西走向的木栈道 AB ,栈道 AB 与景区道路CD 平行.在 C 处测得栈道一端 A 位于北偏西 42°方向,在 D 处测得栈道另一端 B 位于北偏西 32°方向.已知 CD =120 m , BD =80 m ,求木栈道 AB 的长度(结果保留整数) .
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
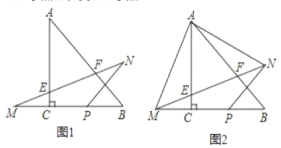
【题目】在Rt△ABC中,∠ACB=90°,AC=BC=2,点P为BC边上的一个动点(不与B.C重合)点P关于直线AC、AB的对称点分别为M、N,连接MN交AC于点E,交AB于点F.
(1)当点P为线段BC的中点时,求∠M的正切值
(2)当点P在线段BC上运动时(不与B.C重合),连接AM、AN,求证:
①△AMN为等腰直角三角形
②△AEF∽△BAM
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线1:y=﹣x+1与x轴、y轴分别交于点B、点E,抛物线L:y=ax2+bx+c经过点B、点A(﹣3,0)和点C(0,﹣3),并与直线l交于另一点D.
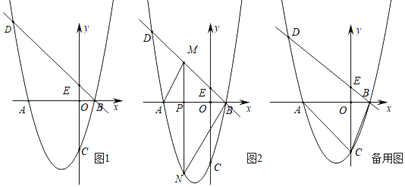
(1)求抛物线L的解析式;
(2)点P为x轴上一动点
①如图2,过点P作x轴的垂线,与直线1交于点M,与抛物线L交于点N.当点P在点A、点B之间运动时,求四边形AMBN面积的最大值;
②连接AD,AC,CP,当∠PCA=∠ADB时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
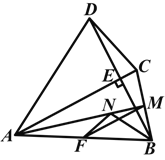
【题目】(2014山东淄博)如图,四边形ABCD中,AC⊥BD交BD于点E,点F,M分别是AB,BC的中点,BN平分∠ABE交AM于点N,AB=AC=BD,连接MF,NF.
(1)判断△BMN的形状,并证明你的结论;
(2)判断△MFN与△BDC之间的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
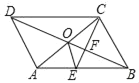
【题目】如图,ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB于点E,交BD于点F,且∠ABC=60°,AB=2BC,连接OE.下列结论:①∠ACD=30°;②SABCD=ACBC;③OE:AC=![]() :6; ④SOEF=
:6; ④SOEF=![]() SABCD,成立的是_____.
SABCD,成立的是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在矩形ABCD中,AB=2,BC=5,∠MPN=90°,且∠MPN的直角顶点在BC边上,BP=1.
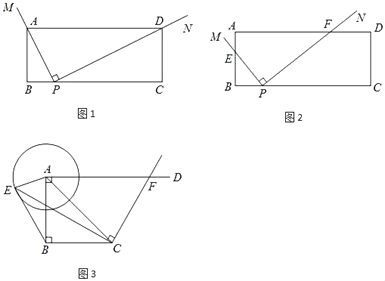
①特殊情形:若MP过点A,NP过点D,则![]() = .
= .
②类比探究:如图2,将∠MPN绕点P按逆时针方向旋转,使PM交AB边于点E,PN交AD边于点F,当点E与点B重合时,停止旋转.在旋转过程中,![]() 的值是否为定值?若是,请求出该定值;若不是,请说明理由.
的值是否为定值?若是,请求出该定值;若不是,请说明理由.
(2)拓展探究:在Rt△ABC中,∠ABC=90°,AB=BC=2,AD⊥AB,⊙A的半径为1,点E是⊙A上一动点,CF⊥CE交AD于点F.请直接写出当△AEB为直角三角形时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】费尔兹奖是国际上享有崇高荣誉的一个数学奖项,每4年评选一次,在国际数学家大会上颁给有卓越贡献的年龄不超过40岁的年轻数学家,美籍华人丘成桐1982年获得费尔兹奖.为了让学生了解费尔兹奖得主的年龄情况,我们查取了截止到2018年60名费尔兹奖得主获奖时的年龄数据,并对数据进行整理、描述和分析.下面给出了部分信息.
a.截止到2018年费尔兹奖得主获奖时的年龄数据的频数分布直方图如图1(数据分成5组,各组是28≤x<31,31≤x<34,34≤x<37,37≤x<40,x≥40):
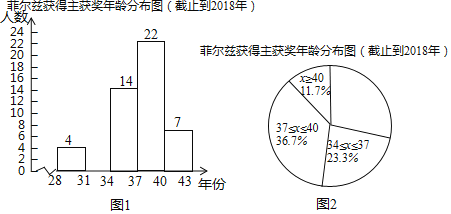
b.如图2,在a的基础上,画出扇形统计图;
c.截止到2018年费尔兹奖得主获奖时的年龄在34≤x<37这一组的数据是:
36 | 35 | 34 | 35 | 35 | 34 | 34 | 35 | 36 | 36 | 36 | 36 | 34 | 35 |
d.截止到2018年时费尔兹奖得主获奖时的年龄的平均数、中位数、众数如下:
年份 | 平均数 | 中位数 | 众数 |
截止到2018 | 35.58 | m | 37,38 |
根据以上信息,回答下列问题:
(1)依据题意,补全频数直方图;
(2)31≤x<34这组的圆心角度数是度,并补全扇形统计图;
(3)统计表中中位数m的值是;
(4)根据以上统计图表试描述费尔兹奖得主获奖时的年龄分布特征.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2014湖南怀化)两个城镇A、B与两条公路ME、MF位置如图所示,其中ME是东西方向的公路.现电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离相等,到两条公路ME、MF的距离也必须相等,且在∠FME的内部.
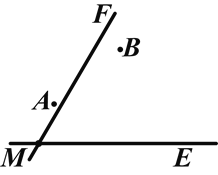
(1)那么点C应选在何处?请在图中,用尺规作图找出符合条件的点C(不写已知、求作、作法,只保留作图痕迹);
(2)设AB的垂直平分线交ME于点N,且![]() km,在M处测得点C位于点M的北偏东60°方向,在N处测得点C位于点N的北偏西45°方向,求点C到公路ME的距离.
km,在M处测得点C位于点M的北偏东60°方向,在N处测得点C位于点N的北偏西45°方向,求点C到公路ME的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com