
【题目】如图,ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB于点E,交BD于点F,且∠ABC=60°,AB=2BC,连接OE.下列结论:①∠ACD=30°;②SABCD=ACBC;③OE:AC=![]() :6; ④SOEF=
:6; ④SOEF=![]() SABCD,成立的是_____.
SABCD,成立的是_____.
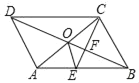
【答案】①②③
【解析】
由四边形ABCD是平行四边形,得到∠ABC=∠ADC=60°,∠BAD=120°,根据角平分线的定义得到∠DCE=∠BCE=60°推出△CBE是等边三角形,证得∠ACB=90°,求出∠ACD=∠CAB=30°,故①正确;由AC⊥BC,得到SABCD=ACBC,故②正确,根据直角三角形的性质得到AC=![]() BC,根据三角形的中位线的性质得到OE=
BC,根据三角形的中位线的性质得到OE=![]() BC,于是得到OE:AC=
BC,于是得到OE:AC=![]() :6;故③正确;根据相似三角形的性质得到
:6;故③正确;根据相似三角形的性质得到![]() =
=![]() =2,求得S△OCF=2S△OEF,所以S△OEF=
=2,求得S△OCF=2S△OEF,所以S△OEF=![]() S△OEC,又因为OE=
S△OEC,又因为OE=![]() BC=
BC=![]() AD,S△OEC= S△OEB,所以S△OEC= S△OEB=
AD,S△OEC= S△OEB,所以S△OEC= S△OEB=![]() S△ABD=
S△ABD=![]() S ABCD,可得:S△OEF=
S ABCD,可得:S△OEF=![]() ×
×![]() S ABCD=
S ABCD=![]() ,故④不正确.
,故④不正确.
解:∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC=60°,∠BAD=120°,
∵CE平分∠BCD交AB于点E,
∴∠DCE=∠BCE=60°
∴△CBE是等边三角形,
∴BE=BC=CE,
∵AB=2BC,
∴AE=BC=CE,
∴∠ACB=90°,
∴∠ACD=∠CAB=30°,故①正确;
∵AC⊥BC,
∴SABCD=ACBC,故②正确,
在Rt△ACB中,∠ACB=90°,∠CAB=30°,
∴AC=![]() BC,
BC,
∵AO=OC,AE=BE,
∴OE=![]() BC,
BC,
∴OE:AC=![]() BC:
BC:![]() BC,
BC,
∴OE:AC=![]() :6;故③正确;
:6;故③正确;
∵AO=OC,AE=BE,
∴OE∥BC,
∴△OEF∽△BCF,![]() =
=![]() =2:1 ,
=2:1 ,
∴S△OCF:S△OEF=![]() =2,
=2,
∴S△OCF=2S△OEF,
∴S△OEF=![]() S△OEC,
S△OEC,
又∵OE=![]() BC=
BC=![]() AD,S△OEC= S△OEB,
AD,S△OEC= S△OEB,
∴ S△OEC= S△OEB=![]() S△ABD=
S△ABD=![]() S ABCD,
S ABCD,
即S△OEF=![]() ×
×![]() S ABCD=
S ABCD=![]() ,
,
故④不正确.
故答案为:①②③.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
【题目】某市长途客运站每天6:30—7:30开往某县的三辆班车票价相同,但车的舒适程度不同.小张和小王因事需在这一时段乘车去该县,但不知道三辆车开来的顺序,两人采用不同的乘车方案:小张无论如何决定乘坐开来的第一辆车,而小王则是先观察后上车,当第一辆车开来时,他不上车,而是仔细观察车的舒适状况.若第二辆车的状况比第一辆车好,他就上第二辆车;若第二辆车不如第一辆车,他就上第三辆车.若按这三辆车的舒适程度分为优、中、差三等,请你思考并回答下列问题:
(1)三辆车按出现的先后顺序共有哪几种可能?
(2)请列表分析哪种方案乘坐优等车的可能性大?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(8,0),O为坐标原点,P是线段OA上任意一点(不含端点O、A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D.当OD=AD=5时,这两个二次函数的最大值之和等于_______
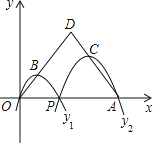
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位射击运动员参加射击训练,各射击20次,成绩如下表所示:
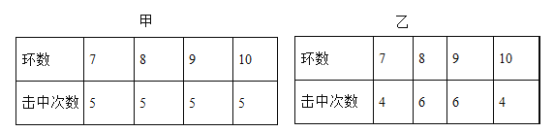
设甲、乙两位运动员射击成绩的方差分别为S 2甲和S 2乙,则下列说法正确的是
A. S 2甲<S 2乙B. S 2甲=S 2乙
C. S 2甲>S 2乙D. 无法比较S 2甲和S 2乙的大小
查看答案和解析>>
科目:初中数学 来源: 题型:
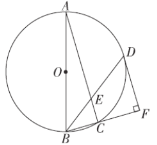
【题目】如图,AB是⊙O的直径,△ABC内接于⊙O.点D在⊙O 上,BD平分∠ABC交AC于点E,DF⊥BC交BC的延长线于点F.
(1)求证:FD是⊙O的切线;
(2)若BD=8,sin∠DBF=![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点 A,B,C,D 依次在同一条直线上,点 E,F 分别在直线 AD 的两侧,已知 BE//CF,∠A=∠D,AE=DF.
(1)求证:四边形 BFCE 是平行四边形.
(2)若 AD=10,EC=3,∠EBD=60°,当四边形 BFCE是菱形时,求 AB 的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
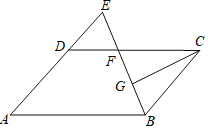
【题目】如图,在平行四边形ABCD中,AB=12,AD=8,∠ABC的平分线交CD于点F,交AD的延长线于点E,CG⊥BE,垂足为G,若EF=2,则线段CG的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
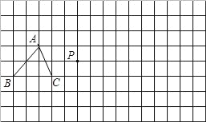
【题目】在下面16×8的正方形网格中,每个小正方形的边长为1个单位,△ABC是格点三角形(顶点在网格交点处),请你画出:
(1)△ABC关于点P的位似△A′B′C′,且位似比为1:2;
(2)以A.B.C.D为顶点的所有格点平行四边形ABCD的顶点D
.
查看答案和解析>>
科目:初中数学 来源: 题型:
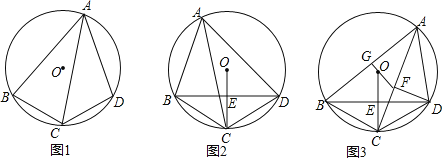
【题目】四边形ABCD内接于⊙O,AC为其中一条对角线,且S△ABC:S△ADC=AB:AD.
(1)如图1,求证:BC=CD;
(2)如图2:连接OC,交对角线BD于点E,若∠BAD=60°,求证:OE=EC;
(3)如图3,在(2)的条件下,过点D作DF⊥AC于点F,连接FO并延长FO,交AB边于点G,若FG⊥AB,OC=![]() ,求△OFC的面积.
,求△OFC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com