
����Ŀ���Ѷ��Ƚ��ǹ��������г��������һ����ѧ���ÿ4����ѡһ�Σ��ڹ�����ѧ�Ҵ���ϰ����Խ�������䲻����40���������ѧ�ң������������ͩ1982���÷Ѷ��Ƚ���Ϊ����ѧ���˽�Ѷ��Ƚ�������������������Dz�ȡ�˽�ֹ��2018��60���Ѷ��Ƚ�������ʱ���������ݣ��������ݽ��������������ͷ�������������˲�����Ϣ��
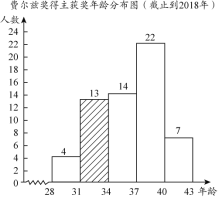
a����ֹ��2018��Ѷ��Ƚ�������ʱ���������ݵ�Ƶ���ֲ�ֱ��ͼ��ͼ1�����ݷֳ�5�飬������28��x��31��31��x��34��34��x��37��37��x��40��x��40����
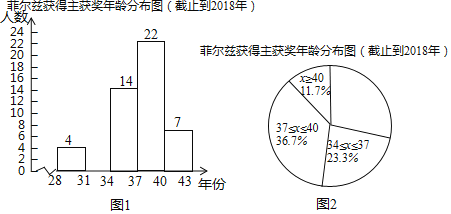
b����ͼ2����a�Ļ����ϣ���������ͳ��ͼ��
c����ֹ��2018��Ѷ��Ƚ�������ʱ��������34��x��37��һ��������ǣ�
36 | 35 | 34 | 35 | 35 | 34 | 34 | 35 | 36 | 36 | 36 | 36 | 34 | 35 |
d����ֹ��2018��ʱ�Ѷ��Ƚ�������ʱ�������ƽ��������λ�����������£�
��� | ƽ���� | ��λ�� | ���� |
��ֹ��2018 | 35.58 | m | 37��38 |
����������Ϣ���ش��������⣺
��1���������⣬��ȫƵ��ֱ��ͼ��
��2��31��x��34�����Բ�ĽǶ����Ƕȣ�����ȫ����ͳ��ͼ��
��3��ͳ�Ʊ�����λ��m��ֵ�ǣ�
��4����������ͳ��ͼ���������Ѷ��Ƚ�������ʱ������ֲ�������
���𰸡���1����ͼ����������2��31��x��34�����Բ�ĽǶ����� 78�ȣ���ȫ����ͳ��ͼ����������3����λ��m��ֵ�� 36����4���𰸲�Ψһ���磺�Ѷ��Ƚ�������ʱ���伯����37����40�꣮
��������
��1������������Ϊ60����ڶ�����������ɽ������;
��2������Բ�Ľ�=360����ٷֱȼ��㼴�ɣ����ݰٷֱȵĺ�Ϊ1������ڶ���İٷֱȣ����ɻ�������ͳ��ͼ;
��3��������λ���Ķ��壬��λ�����ڵ�30��31�������ƽ����;
��4���𰸲�Ψһ���������ɣ�
��1����ͼ��
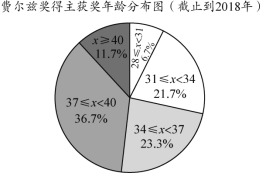
��2��31��x��34�����Բ�ĽǶ���=360���21.7%��78��;
��3����λ�����ڵ�30��31�������ƽ��������30��31������λ��34��x��37������2����Ϊ36,36����ͳ�Ʊ�����λ��m��ֵ�� 36��
��4���𰸲�Ψһ���磺�Ѷ��Ƚ�������ʱ���伯����37����40�꣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+c��a��0����ͼ����ͼ�����������ĸ����ۣ���4ac��b2��0����4a+c��2b����3b+2c��0����m��am+b��+b��a��m�٩�1����������ȷ���۵ĸ����ǣ� ��
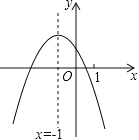
A.4��B.3��C.2��D.1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��B�Ƿ���������y��![]() ��k��0��ͼ���ϵ����㣬�ӳ��߶�AB��y���ڵ�C���ҵ�BΪ�߶�AC�е㣬����A��AD��x���ڵ�D����EΪ�߶�OD�����ȷֵ㣬��OE��DE������AE��BE����S��ABE��7����k��ֵΪ�� ��
��k��0��ͼ���ϵ����㣬�ӳ��߶�AB��y���ڵ�C���ҵ�BΪ�߶�AC�е㣬����A��AD��x���ڵ�D����EΪ�߶�OD�����ȷֵ㣬��OE��DE������AE��BE����S��ABE��7����k��ֵΪ�� ��
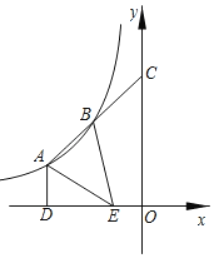
A.��12B.��10C.��9D.��6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����ֱ����OAB��б��OB��x���ϣ���OB��4������������y��![]() ��x��0����ͼ��OA���е�C����AB�ڵ�D�����D������_____��
��x��0����ͼ��OA���е�C����AB�ڵ�D�����D������_____��
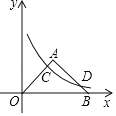
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������Աij��Ĺ��������ͼ��ʾ�����е�![]() ��
��![]() ��
��![]() �ĺᡢ������ֱ��ʾ�ס��ҡ����������Ա�������Ϳ�����õ�ʱ��ͼ�������
�ĺᡢ������ֱ��ʾ�ס��ҡ����������Ա�������Ϳ�����õ�ʱ��ͼ�������![]() ��
��![]() ��
��![]() ���ĺᡢ������ֱ��ʾ�ס��ҡ����������Ա�������Ϳ�����õ�ʱ��ͼ���.�������������ۣ����������Ϳ������ʱ����̵��Ǽף����������Ϳ�ݼ��������DZ���������һ�������Ϳ���ܼ�����������.���������У�������ȷ���۵�����ǣ� ��
���ĺᡢ������ֱ��ʾ�ס��ҡ����������Ա�������Ϳ�����õ�ʱ��ͼ���.�������������ۣ����������Ϳ������ʱ����̵��Ǽף����������Ϳ�ݼ��������DZ���������һ�������Ϳ���ܼ�����������.���������У�������ȷ���۵�����ǣ� ��
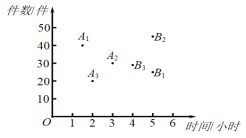
A. �٢�B. �٢�C. ��D. �ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ����λ��������λ�����ֵĺ͵�����һ����λ�ϵ����֣���������λ��Ϊ��������λ�������ִ�1��2��3��4��5��5����������ȡ�������֣�������ظ������Ұ�λ���֡�ʮλ���֡���λ���������������λ����
��1�����оٳ����п��ܵõ�����λ����
��2��С����С����һ����Ϸ����Ϸ�������£�����1������ɵ���λ���ǡ�������λ��������С��ʤ������С��ʤ�������Ϸ��ƽ��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪Rt��ABC�У�CAB=60�㣬��OΪб��AB��һ�㣬��OA=2����OAΪ�뾶����O��BC������D����AC���ڵ�E������AD��
��1�����߶�CD�ij���
��2������O��Rt��ABC�ص����ֵ���������������ȷֵ��
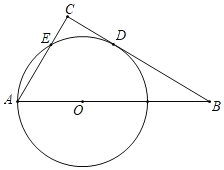
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У�E��F�ֱ�Ϊ��AB��CD���е㣬BD�ǶԽ��ߣ�
��1����֤����ADE�ա�CBF��
��2������ADB��ֱ�ǣ����ı���BEDF��ʲô�ı��Σ�֤����Ľ��ۣ�
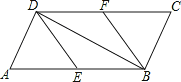
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ���ھ���ABCD�У���E�ڱ�AD�ϣ���F�ڱ�BC�ϣ���AE=CF����EG��FH���ֱ���Խ���BD���ڵ�G��H������EH��FG��
��1����֤����BFH�ա�DEG��
��2������DF����BF=DF�����ı���EGFH��ʲô�����ı��Σ�֤����Ľ��ۣ�
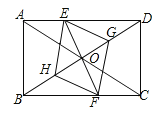
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com