
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 轴,且直线l与抛物线
轴,且直线l与抛物线![]() 和y轴分别交于点A,B,C,点D为抛物线的顶点.若点E的坐标为
和y轴分别交于点A,B,C,点D为抛物线的顶点.若点E的坐标为![]() ,点A的横坐标为1.
,点A的横坐标为1.
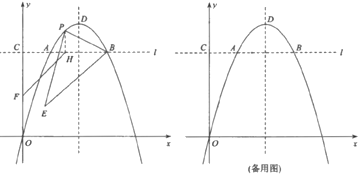
(1)线段AB的长度等于________;
(2)点P为线段AB上方抛物线上的一点,过点P作AB的垂线交AB于点H,点F为y轴上一点,当![]() 的面积最大时,求
的面积最大时,求![]() 的最小值;
的最小值;
(3)在(2)的条件下,删除抛物线![]() 在直线PH左侧部分图象并将右侧部分图象沿直线PH翻折,与抛物线在直线PH右侧部分图象组成新的函数M的图象.现有平行于FH的直线
在直线PH左侧部分图象并将右侧部分图象沿直线PH翻折,与抛物线在直线PH右侧部分图象组成新的函数M的图象.现有平行于FH的直线![]() ,若直线
,若直线![]() 与函数M的图象有且只有2个交点,求t的取值范围(请直接写出t的取值范围,无需解答过程).
与函数M的图象有且只有2个交点,求t的取值范围(请直接写出t的取值范围,无需解答过程).
【答案】(1)2 (2) ![]() (3) t的取值范围为:t<
(3) t的取值范围为:t<![]() .
.
【解析】
(1)先求抛物线y=-x2+4x的对称轴,由于已知点A的坐标,再利用对称性可求点B坐标;从而得AB的长度;
(2)先根据B和E坐标得出BE的解析式,然后设与其平行的直线为y=x+b,过点H作y=-x的垂线,可求得HF和FO,从而得解;
(3)可根据顶点位置的变动,得出抛物线y=-x2+4x右侧部分图象沿直线PH翻折后抛物线的解析式;由(2)FH直线解析式,平行于FH的直线l1:y=mx+t,其m值可求;令y=mx+t与翻折后抛物线相切,可求得t的临界值,结合图象可得最后答案.
解:(1)抛物线y=﹣x2+4x的对称轴为直线![]() .
.
∵点A的横坐标为1.代入y=﹣x2+4x得:y=3,
∴A(1,3),由抛物线的对称性得:点B的坐标为(3,3).
∴AB=2.
故答案为:2.
(2)∵B(3,3),E(1,1),
∴直线BE解析式为y=x,作l∥BE,且与抛物线相切,则可设l的解析式为:y=x+b.根据该直线与抛物线相切,列一元二次方程,令其判别式为0,可求得b的值,从而得点P的坐标,进而得点H坐标及PH长,
∴x+b=﹣x2+4x,即x2﹣3x+b=0,
∴△=9﹣4b=0,b=![]() ,
,
∴x2﹣3x+![]() =0,
=0,
∴切点为:x=![]() ,y=
,y=![]() ,
,
∴PH=![]() ﹣3=
﹣3=![]()
过点H作y=﹣x的垂线,交y=﹣x于点G,交y轴于点F,则GF=![]() FO,∠FGO=∠OFG=∠CFH=∠CHF=45°,
FO,∠FGO=∠OFG=∠CFH=∠CHF=45°,
![]()
![]()
![]() .
.
∴PH+HF+![]() FO的最小值为:
FO的最小值为:![]() .
.
(3)在(2)的条件下,平行于FH的直线l1:y=mx+t,若直线l1与函数M的图象有且只有2个交点,
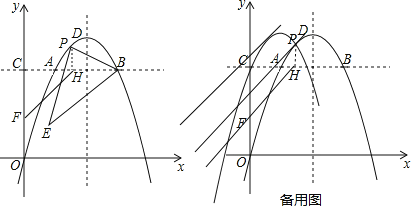
∵∠CFH=45°,l1∥FH,
∴m=1,y=x+t,
∵抛物线y=﹣x2+4x的顶点D为(2,4),点H为(![]() ,3)点P为(
,3)点P为(![]() ,
,![]() ),
),
∴抛物线y=﹣x2+4x右侧部分图象沿直线PH翻折后抛物线顶点为(1,4),其解析式为y=﹣x2+2x+3.
当直线y=x+t与抛物线y=﹣x2+2x+3相切时,x+t=﹣x2+2x+3,
∴x2﹣x+t﹣3=0,△=1﹣4(t﹣3)=13﹣4t=0
∴t=![]() ;
;
∴t<![]() 时直线l1与函数M的图象有且只有2个交点.
时直线l1与函数M的图象有且只有2个交点.
∴t的取值范围为:t<![]() .
.


 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】如图(1)是一款手机支架,忽略支管的粗细,得到它的简化结构图如图(2)所示.已知支架底部支架CD平行于水平面,EF⊥OE,GF⊥EF,支架可绕点O旋转,OE=20cm,EF=20![]() cm.如图(3)若将支架上部绕O点逆时针旋转,当点G落在直线CD上时,测量得∠EOG=65°.
cm.如图(3)若将支架上部绕O点逆时针旋转,当点G落在直线CD上时,测量得∠EOG=65°.
(1)求FG的长度(结果精确到0.1);
(2)将支架由图(3)转到图(4)的位置,若此时F、O两点所在的直线恰好于CD垂直,点F的运动路线的长度称为点F的路径长,求点F的路径长.
(参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14,1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某旅游景区为方便游客,修建了一条东西走向的木栈道 AB ,栈道 AB 与景区道路CD 平行.在 C 处测得栈道一端 A 位于北偏西 42°方向,在 D 处测得栈道另一端 B 位于北偏西 32°方向.已知 CD =120 m , BD =80 m ,求木栈道 AB 的长度(结果保留整数) .
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
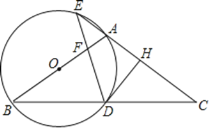
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC,垂足为点H,连接DE,交AB于点F.
(1)求证:DH是⊙O的切线;
(2)若⊙O的半径为4,
①当AE=FE时,求![]() 的长(结果保留π);
的长(结果保留π);
②当![]() 时,求线段AF的长.
时,求线段AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)(x+y)2-2x(x+y); (2)(a+1)(a-1)-(a-1)2;
(3)先化简,再求值:
(x+2y)(x-2y)-(2x3y-4x2y2)÷2xy,其中x=-3,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若一次函数y=ax+b和反比例函数y=-![]() 满足a+c=2b,则称为y=ax2+bx+c为一次函数和反比例函数的“等差”函数.
满足a+c=2b,则称为y=ax2+bx+c为一次函数和反比例函数的“等差”函数.
(1)判断y=x+b和y=-![]() 是否存在“等差”函数?若存在,写出它们的“等差”函数;
是否存在“等差”函数?若存在,写出它们的“等差”函数;
(2)若y=5x+b和y=-![]() 存在“等差”函数,且“等差”函数的图象与y=-
存在“等差”函数,且“等差”函数的图象与y=-![]() 的图象的一个交点的横坐标为1,求一次函数和反比例函数的表达式;
的图象的一个交点的横坐标为1,求一次函数和反比例函数的表达式;
(3)若一次函数y=ax+b和反比例函数y=-![]() (其中a>0,c>0,a=
(其中a>0,c>0,a=![]() b)存在“等差”函数,且y=ax+b与“等差”函数有两个交点A(x1,y1)、B(x2,y2),试判断“等差”函数图象上是否存在一点P(x,y)(其中x1<x<x2),使得△ABP的面积最大?若存在,用c表示△ABP的面积的最大值;若不存在,请说明理由.
b)存在“等差”函数,且y=ax+b与“等差”函数有两个交点A(x1,y1)、B(x2,y2),试判断“等差”函数图象上是否存在一点P(x,y)(其中x1<x<x2),使得△ABP的面积最大?若存在,用c表示△ABP的面积的最大值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
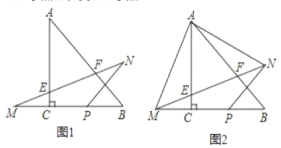
【题目】在Rt△ABC中,∠ACB=90°,AC=BC=2,点P为BC边上的一个动点(不与B.C重合)点P关于直线AC、AB的对称点分别为M、N,连接MN交AC于点E,交AB于点F.
(1)当点P为线段BC的中点时,求∠M的正切值
(2)当点P在线段BC上运动时(不与B.C重合),连接AM、AN,求证:
①△AMN为等腰直角三角形
②△AEF∽△BAM
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线1:y=﹣x+1与x轴、y轴分别交于点B、点E,抛物线L:y=ax2+bx+c经过点B、点A(﹣3,0)和点C(0,﹣3),并与直线l交于另一点D.
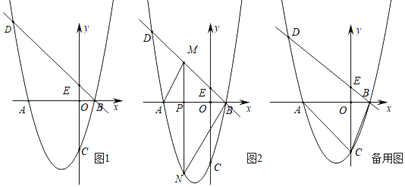
(1)求抛物线L的解析式;
(2)点P为x轴上一动点
①如图2,过点P作x轴的垂线,与直线1交于点M,与抛物线L交于点N.当点P在点A、点B之间运动时,求四边形AMBN面积的最大值;
②连接AD,AC,CP,当∠PCA=∠ADB时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】费尔兹奖是国际上享有崇高荣誉的一个数学奖项,每4年评选一次,在国际数学家大会上颁给有卓越贡献的年龄不超过40岁的年轻数学家,美籍华人丘成桐1982年获得费尔兹奖.为了让学生了解费尔兹奖得主的年龄情况,我们查取了截止到2018年60名费尔兹奖得主获奖时的年龄数据,并对数据进行整理、描述和分析.下面给出了部分信息.
a.截止到2018年费尔兹奖得主获奖时的年龄数据的频数分布直方图如图1(数据分成5组,各组是28≤x<31,31≤x<34,34≤x<37,37≤x<40,x≥40):
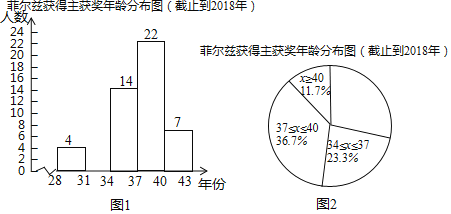
b.如图2,在a的基础上,画出扇形统计图;
c.截止到2018年费尔兹奖得主获奖时的年龄在34≤x<37这一组的数据是:
36 | 35 | 34 | 35 | 35 | 34 | 34 | 35 | 36 | 36 | 36 | 36 | 34 | 35 |
d.截止到2018年时费尔兹奖得主获奖时的年龄的平均数、中位数、众数如下:
年份 | 平均数 | 中位数 | 众数 |
截止到2018 | 35.58 | m | 37,38 |
根据以上信息,回答下列问题:
(1)依据题意,补全频数直方图;
(2)31≤x<34这组的圆心角度数是度,并补全扇形统计图;
(3)统计表中中位数m的值是;
(4)根据以上统计图表试描述费尔兹奖得主获奖时的年龄分布特征.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com