
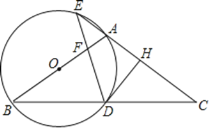
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC,垂足为点H,连接DE,交AB于点F.
(1)求证:DH是⊙O的切线;
(2)若⊙O的半径为4,
①当AE=FE时,求![]() 的长(结果保留π);
的长(结果保留π);
②当![]() 时,求线段AF的长.
时,求线段AF的长.
【答案】(1)详见解析;(2)①![]() ;②
;②![]()
【解析】
(1)根据同圆的半径相等和等边对等角证明:∠ODB=∠OBD=∠ACB,则DH⊥OD,DH是圆O的切线;
(2)①根据等腰三角形的性质的∠EAF=∠EAF,设∠B=∠C=α,得到∠EAF=∠EFA=2α,根据三角形的内角和得到∠B=36°,求得∠AOD=72°,根据弧长公式即可得到结论;
②连接AD,根据圆周角定理得到∠ADB=∠ADC=90°,解直角三角形得到AD=![]() ,根据相似三角形的性质得到AH=3,于是得到结论.
,根据相似三角形的性质得到AH=3,于是得到结论.
证明:(1)连接OD,如图,

∵OB=OD,
∴△ODB是等腰三角形,
∠OBD=∠ODB①,
在△ABC中,∵AB=AC,
∴∠ABC=∠ACB②,
由①②得:∠ODB=∠OBD=∠ACB,
∴OD∥AC,
∵DH⊥AC,
∴DH⊥OD,
∴DH是圆O的切线;
(2)①∵AE=EF,
∴∠EAF=∠EAF,
设∠B=∠C=α,
∴∠EAF=∠EFA=2α,
∵∠E=∠B=α,
∴α+2α+2α=180°,
∴α=36°,
∴∠B=36°,
∴∠AOD=72°,
∴![]() 的长=
的长=![]() ;
;
②连接AD,
∵AB为⊙O的直径,
∴∠ADB=∠ADC=90°,
∵⊙O的半径为4,
∴AB=AC=8,
∵![]() ,
,
∴![]() ,
,
∴AD=![]() ,
,
∵AD⊥BC,DH⊥AC,
∴△ADH∽△ACD,
∴![]() ,
,
∴![]() ,
,
∴AH=3,
∴CH=5,
∵∠B=∠C,∠E=∠B,
∴∠E=∠C,
∴DE=DC,∵DH⊥AC,
∴EH=CH=5,
∴AE=2,
∵OD∥AC,
∴∠EAF=∠FOD,∠E=∠FDO,
∴△AEF∽△ODF,
∴![]() ,
,
∴![]() ,
,
∴AF=![]() .
.


科目:初中数学 来源: 题型:
【题目】某校为了解九年级全体学生物理实验操作的情况,随机抽取了30名学生的物理实验操作考核成绩,并将数据进行整理,分析如下: (说明:考核成绩均取整数,A级:10分,B级:9分,C级:8分,D级:7分及以下)
收集数据
10,8,10,9,5,10,9,9,10,8,9,10,9,9,8,9,8,10,7,9,8,10,9,6,9,10,9,10,8,10
整理数据
整理、描述样本数据,绘制统计表如下:
抽取的30名学生物理实验操作考核成绩频数统计表
成绩等级 | A | B | C | D |
人数(名) | 10 | m | n | 3 |
根据表中的信息,解答下列问题:
(1)m=________,n=________;
(2)若该校九年级共有800名学生参加物理实验操作考核,成绩不低于9分为优秀,试估计该校九年级参加物理实验操作考核成绩达到优秀的学生有多少名?
(3)甲、乙、丙、丁是九年级1班物理实验考核成绩为10分的四名学生,学校计划从这四名学生中随机选出两名学生代表学校去参加全市中学生“物理实验操作”竞赛,用列表法或画树状图法,求甲、乙两名学生中至少有一名被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
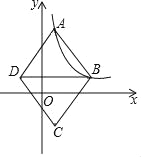
【题目】如图,在平面直角坐标系中,菱形ABCD的顶点A、B在反比例函数y=![]() (k>0,x>0)的图象上,横坐标分别为1,4,对角线BD∥x轴.若菱形ABCD的面积为
(k>0,x>0)的图象上,横坐标分别为1,4,对角线BD∥x轴.若菱形ABCD的面积为![]() ,则k的值为_____.
,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数解析式为y=(m-2) ![]()
(1)若函数为正比例函数,试说明函数y随x增大而减小
(2)若函数为二次函数,写出函数解析式,并写出开口方向
(3)若函数为反比例函数,写出函数解析式,并说明函数在第几象限
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,点P为BC上任意一点(可与点B或C重合),分别过B、C、D作射线AP的垂线,垂足分别是B′、C′、D′,则BB′+CC′+DD′的最小值是( )
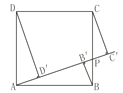
A. 1 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司准备投资开发A、B两种新产品,通过市场调研发现:如果单独投资A种产品,则所获利润yA(万元)与投资金额x(万元)之间满足正比例函数关系:yA=kx;如果单独投资B种产品,则所获利润yB(万元)与投资金额x(万元)之间满足二次函数关系:yB=ax2+bx.根据公司信息部的报告,yA、yB(万元)与投资金额x(万元)的部分对应值(如下表)

(1)求正比例函数和二次函数的解析式;
(2)如果公司准备投资20万元同时开发A、B两种新产品,请你设计一个能获得最大利润的投资方案,并求出按此方案能获得的最大利润是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() ,直线
,直线![]() 与y轴交于点A,与双曲线
与y轴交于点A,与双曲线![]() 交于点
交于点![]() .
.
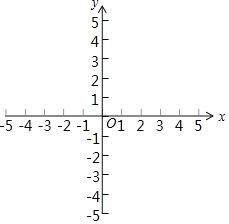
(1)求点B的坐标及k的值;
(2)将直线AB平移,使它与x轴交于点C,与y轴交于点D,若![]() 的面积为6,求直线CD的表达式.
的面积为6,求直线CD的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等.交易其一,金轻十三两.问金、银一枚各重几何?”.意思是:甲袋中装有黄金9枚(每枚黄金重量相同),乙袋中装有白银11枚(每枚白银重量相同),称重两袋相等.两袋互相交换1枚后,甲袋比乙袋轻了13两(袋子重量忽略不计).问黄金、白银每枚各重多少两?设每枚黄金重x两,每枚白银重y两,根据题意得( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂准备用图甲所示的A型正方形板材和B型长方形板材,制作成图乙所示的竖式和横式两种无盖箱子.
![]() 若该工厂准备用不超过10000元的资金去购买A,B两种型号板材,并全部制作竖式箱子,已知A型板材每张30元,B型板材每张90元,求最多可以制作竖式箱子多少只?
若该工厂准备用不超过10000元的资金去购买A,B两种型号板材,并全部制作竖式箱子,已知A型板材每张30元,B型板材每张90元,求最多可以制作竖式箱子多少只?
![]() 若该工厂仓库里现有A型板材65张、B型板材110张,用这批板材制作两种类型的箱子,问制作竖式和横式两种箱子各多少只,恰好将库存的板材用完?
若该工厂仓库里现有A型板材65张、B型板材110张,用这批板材制作两种类型的箱子,问制作竖式和横式两种箱子各多少只,恰好将库存的板材用完?
![]() 若该工厂新购得65张规格为
若该工厂新购得65张规格为![]() 的C型正方形板材,将其全部切割成A型或B型板材
的C型正方形板材,将其全部切割成A型或B型板材![]() 不计损耗
不计损耗![]() ,用切割成的板材制作两种类型的箱子,要求竖式箱子不少于20只,且材料恰好用完,则能制作两种箱子共______只
,用切割成的板材制作两种类型的箱子,要求竖式箱子不少于20只,且材料恰好用完,则能制作两种箱子共______只![]()

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com