
【题目】某公司准备投资开发A、B两种新产品,通过市场调研发现:如果单独投资A种产品,则所获利润yA(万元)与投资金额x(万元)之间满足正比例函数关系:yA=kx;如果单独投资B种产品,则所获利润yB(万元)与投资金额x(万元)之间满足二次函数关系:yB=ax2+bx.根据公司信息部的报告,yA、yB(万元)与投资金额x(万元)的部分对应值(如下表)

(1)求正比例函数和二次函数的解析式;
(2)如果公司准备投资20万元同时开发A、B两种新产品,请你设计一个能获得最大利润的投资方案,并求出按此方案能获得的最大利润是多少万元?
【答案】(1)yA=0.6x,yB=﹣0.2x2+3x;(2)投资6万元生产B产品,14万元生产A产品可获得最大利润19.2万元.
【解析】试题分析:(1)根据表格提供的数据,列方程组易求出表达式;
(2)设投资开发B产品的金额为x万元,总利润y万元,列出利润表达式,运用函数性质解答即可.
试题解析:解:(1)把点(1,0.6)代入yA=kx中,得:k=0.6,则该正比例函数的解析式为:yA=0.6x,把点(1,2.8)和点(5,10)代入yB=ax2+bx.得:![]() ,解得:
,解得:![]() ,则该二次函数的解析式为:yB=﹣0.2x2+3x;
,则该二次函数的解析式为:yB=﹣0.2x2+3x;
(2)设投资开发B产品的金额为x万元,总利润为y万元,则y=0.6x(20﹣x)+(﹣0.2x2+3x)
=﹣0.2x2+2.4x+12=﹣0.2(x﹣6)2+19.2
∴当x=6时,y最大=19.2.
答:投资6万元生产B产品,14万元生产A产品可获得最大利润19.2万元.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】小慧根据学习函数的经验,对函数y=|x﹣1|的图象与性质进行了探究.下面是小慧的探究过程,请补充完成:
(1)函数y=|x﹣1|的自变量x的取值范围是 ;
(2)列表,找出y与x的几组对应值.
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | b | 1 | 0 | 1 | 2 | … |
其中,b= ;
(3)在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;
(4)写出该函数的一条性质: .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是菱形,AB=4,∠ABC=60°,∠EAF的两边分别与射线CB,DC相交于点E,F,且∠EAF=60°.

(1)如图1,当点E是线段CB的中点时,直接写出线段AE,EF,AF之间的数量关系;
(2)如图2,当点E是线段CB上任意一点时(点E不与B、C重合),求证:BE=CF;
(3)如图3,当点E在线段CB的延长线上,且∠EAB=15°时,求点F到BC的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
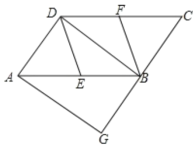
【题目】如图,在平行四边形ABCD中,E、 F分别为边AB、CD的中点,BD是对角线.过点有作AG∥DB交CB的延长线于点G.
(1)求证:△ADE≌△CBF;
(2)若∠G=90° ,求证:四边形DEBF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.
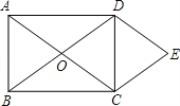
(1)试判断四边形OCED的形状,并说明理由;
(2)若AB=6,BC=8,求四边形OCED的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
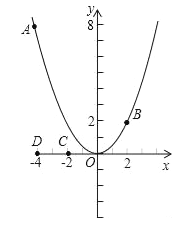
【题目】如图,已知点A(﹣4,8)和点B(2,n)在抛物线y=ax2上.
(1)求a的值及点B关于x轴对称点P的坐标,并在x轴上找一点Q,使得AQ+QB最短,求出点Q的坐标;
(2)平移抛物线y=ax2,记平移后点A的对应点为A′,点B的对应点为B′,点C(﹣2,0)和点D(﹣4,0)是x轴上的两个定点.
①当抛物线向左平移到某个位置时,A′C+CB′最短,求此时抛物线的函数解析式;
②当抛物线向左或向右平移时,是否存在某个位置,使四边形A′B′CD的周长最短?若存在,求出此时抛物线的函数解析式;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把边长为1的正方形ABCD绕顶点A逆时针旋转30°到正方形AB′C′D′,则它们的公共部分的面积等于_____.
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/13/1923101670465536/1923902127538176/STEM/3534c7f6f1a5489684ae6308493b71da.png]
查看答案和解析>>
科目:初中数学 来源: 题型:
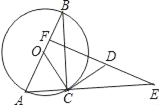
【题目】如图,⊙O是Rt△ABC的外接圆,AB为直径,∠ABC=30°,CD是⊙O的切线,E为AC延长线上一点,ED⊥AB于F.
(1)判断△DCE的形状;
(2)设⊙O的半径为1,且OF=![]() ,求证:△DCE≌△OCB.
,求证:△DCE≌△OCB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com