
【题目】如图,⊙O是Rt△ABC的外接圆,AB为直径,∠ABC=30°,CD是⊙O的切线,E为AC延长线上一点,ED⊥AB于F.
(1)判断△DCE的形状;
(2)设⊙O的半径为1,且OF=![]() ,求证:△DCE≌△OCB.
,求证:△DCE≌△OCB.
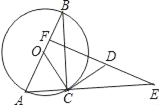
【答案】(1)△CDE为等腰三角形;(2)证明见解析.
【解析】试题分析:(1)由∠ABC=30°可得∠BAC=60°,结合DE⊥AB,可得∠AED的度数;根据弦切角定理可得∠DCB=60°,再结合∠ACB=90°,从而可得∠DCE的度数;
(2)由(1)的证明过程可得∠ABC=∠OCB=∠DCE=∠CED=30°,要证明△BOC≌△EDC,只要证明BC=CE,接下来由圆半径为1可得AB的长,结合含30度角直角三角形的性质以及勾股定理可得AC、BC的长,在Rt△AEF中,先求得AF的长,再利用含30度角直角三角形的性质可得AE的长,继而得到CE的长,从而可证△CDE≌△COB..
(1)解:∵∠ABC=30°,
∴∠BAC=60°.
又∵OA=OC,
∴△AOC是正三角形.
又∵CD是切线,
∴∠OCD=90°.
∴∠DCE=180°﹣60°﹣90°=30°.
而ED⊥AB于F,
∴∠CED=90°﹣∠BAC=30°.
故△CDE为等腰三角形.
(2)证明:∵CD是⊙O的切线,
∴∠OCD=90°,
∵∠BAC=60°,AO=CO,
∴∠OCA=60°,∵∠DCE=30°.
∴A,C,E三点同线
在△ABC中,
∵AB=2,AC=AO=1,
∴BC=![]() =
=![]() .
.
∵OF=![]() ,
,
∴AF=AO+OF=![]() .
.
又∵∠AEF=30°,
∴AE=2AF=![]() +1,
+1,
∴CE=AE﹣AC=![]() =BC,
=BC,
而∠OCB=∠ACB﹣∠ACO=90°﹣60°=30°=∠ABC;
故△CDE≌△COB.


科目:初中数学 来源: 题型:
【题目】某公司准备投资开发A、B两种新产品,通过市场调研发现:如果单独投资A种产品,则所获利润yA(万元)与投资金额x(万元)之间满足正比例函数关系:yA=kx;如果单独投资B种产品,则所获利润yB(万元)与投资金额x(万元)之间满足二次函数关系:yB=ax2+bx.根据公司信息部的报告,yA、yB(万元)与投资金额x(万元)的部分对应值(如下表)

(1)求正比例函数和二次函数的解析式;
(2)如果公司准备投资20万元同时开发A、B两种新产品,请你设计一个能获得最大利润的投资方案,并求出按此方案能获得的最大利润是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
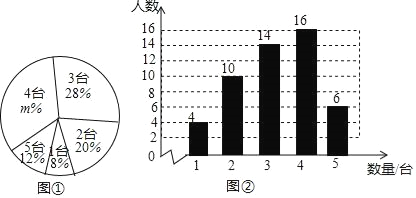
【题目】随着移动计算技术和无线网络的快速发展,移动学习方式越来越引起人们的关注,某校计划将这种学习方式应用到教育学中,从全校1500名学生中随机抽取了部分学生,对其家庭中拥有的移动设备的情况进行调查,并绘制出如下的统计图①和图②,根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的学生人数为 ,图①中m的值为 ;
(2)求本次调查获取的样本数据的众数、中位数和平均数;
(3)根据样本数据,估计该校1500名学生家庭中拥有3台移动设备的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:探究一次函数y=kx+k+2(k是不为0常数)图象的共性特点,探究过程:小明尝试把x=-1代入时,发现可以消去k,竟然求出了y=2.老师问:结合一次函数图象,这说明了什么?小组讨论得出:无论k取何值,一次函数y=kx+k+2的图象一定经过定点(-1,2),老师:如果一次函数的图象是经过某一个定点的直线,那么我们把像这样的一次函数的图象定义为“点旋转直线”.已知一次函数y=(k+3)x+(k-1)的图象是“点旋转直线”
(1)一次函数y=(k+3)x+(k-1)的图象经过的定点P的坐标是__________.
(2)已知一次函数y=(k+3)x+(k-1)的图象与x轴、y轴分别相交于点A、B
①若△OBP的面积为3,求k值;
②若△AOB的面积为1,求k值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】做大小两个长方体纸盒,尺寸如下(单位:cm)
长 | 宽 | 高 | |
小纸盒 |
|
|
|
大纸盒 |
|
|
|
(1)做这两个纸盒共用料多少平方厘米?
(2)做大纸盒比做小纸盒多用料多少平方厘米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校根据课程设置要求,开设了数学类拓展性课程,为了解学生最喜欢的课程内容,随机抽取了部分学生进行问卷调查(每人必须且只选中其中一项),并将统计结果绘制成如下统计图(不完整),请根据图中信息回答问题:

(1)求m,n的值.
(2)补全条形统计图.
(3)该校共有1200名学生,试估计全校最喜欢“数学史话”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E为AB上的点(不与A,B重合),△ADE与△FDE关于DE对称,作射线CF,与DE的延长线相交于点G,连接AG,

(1)当∠ADE=15°时,求∠DGC的度数;
(2)若点E在AB上移动,请你判断∠DGC的度数是否发生变化,若不变化,请证明你的结论;若会发生变化,请说明理由;
(3)如图2, 当点F落在对角线BD上时,点M为DE的中点,连接AM,FM,请你判断四边形AGFM的形状,并证明你的结论。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com