
����Ŀ�����⣺̽��һ�κ���y=kx+k+2��k�Dz�Ϊ0������ͼ��Ĺ����ص㣬̽�����̣�С������x=-1����ʱ�����ֿ�����ȥk����Ȼ�����y=2����ʦ�ʣ����һ�κ���ͼ����˵����ʲô��С�����۵ó�������kȡ��ֵ��һ�κ���y=kx+k+2��ͼ��һ���������㣨-1��2������ʦ�����һ�κ�����ͼ���Ǿ���ijһ�������ֱ�ߣ���ô���ǰ���������һ�κ�����ͼ����Ϊ������תֱ��������֪һ�κ���y=��k+3��x+��k-1����ͼ����������תֱ����
��1��һ�κ���y=��k+3��x+��k-1����ͼ���Ķ���P��������__________��
��2����֪һ�κ���y=��k+3��x+��k-1����ͼ����x�ᡢy��ֱ��ཻ�ڵ�A��B
������OBP�����Ϊ3����kֵ��
������AOB�����Ϊ1����kֵ��
���𰸡���1����-1��-4������2����k=7��-5����k=5��-1��
��������
��1���Ȱ�һ�κ���y=��k+3��x+��k-1������Ϊy=k��x+1��+3x-1����ʽ������x+1=0�����y��ֵ���ɣ�
��2������k��ʾ��AB�����꣬�ٸ��������ε������ʽ���ɵó����ۣ�
��1����һ�κ���y=��k+3��x+��k-1������Ϊy=k��x+1��+3x-1����ʽ��
����x+1=0����x=-1��
��y=-4��
��P��-1��-4����
�ʴ�Ϊ����-1��-4����
��2����һ�κ���y=��k+3��x+��k-1����ͼ����x�ᡢy��ֱ��ཻ�ڵ�A��B
��A��![]() ��0����B��0��k-1����
��0����B��0��k-1����
�١ߡ�OBP�����Ϊ3��
��![]() |k-1|=3�����k=7��-5��
|k-1|=3�����k=7��-5��
�ڡߡ�AOB�����Ϊ1��
��![]() ��|k-1|��|
��|k-1|��|![]() |=1�����k=5��-1��
|=1�����k=5��-1��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
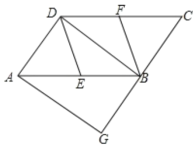
����Ŀ����ͼ����ƽ���ı���ABCD�У�E�� F�ֱ�Ϊ��AB��CD���е㣬BD�ǶԽ���.��������AG��DB��CB���ӳ����ڵ�G.
(1)��֤����ADE�ա�CBF��
(2)����G=90�� ,��֤:�ı���DEBF������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ж������ֻ���ӣ���������Ϊ10t��ÿֻ���ӵ�����������1t��Ϊ��֤�ܰ���Щ����һ�����ߣ���������Ҫ����������3t��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲�����ĵ���ͼ����Ӧ�ĵ�ʽ��̽�����еĹ��ɣ�
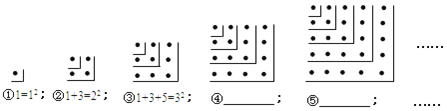
��1���ڢܺ͢ݺ���ĺ����Ϸֱ�д����Ӧ�ĵ�ʽ��
��2�����ú���n��ʽ�ӱ�ʾ��n����ʽ���� ������nΪ��������
��3�������������ɼ��㣺
��1+3+5+��+49��
��101+103+105+��+197+199��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2015���ݣ���ͼ����֪������C1��![]() ��C2��
��C2��![]() ������ԭ�㣬����ֱ�ΪA��B����x�����һ����ֱ�ΪM��N�������A���B����M���N������ԭ��O�����ĶԳƣ����������C1��C2Ϊ���������ߣ�����д��һ�Խ���������C1��C2��ʹ�ı���ANBMǡ���Ǿ��Σ�����д��һ�������߽���ʽ��____________________��__________________��
������ԭ�㣬����ֱ�ΪA��B����x�����һ����ֱ�ΪM��N�������A���B����M���N������ԭ��O�����ĶԳƣ����������C1��C2Ϊ���������ߣ�����д��һ�Խ���������C1��C2��ʹ�ı���ANBMǡ���Ǿ��Σ�����д��һ�������߽���ʽ��____________________��__________________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����OABC�Ķ���A��C������ֱ�Ϊ��10��0������0��4������D��OA���е㣬��P��BC���˶�������ODP������Ϊ5�ĵ���������ʱ����P������Ϊ______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
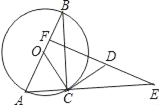
����Ŀ����ͼ����O��Rt��ABC�����Բ��ABΪֱ������ABC=30�㣬CD�ǡ�O�����ߣ�EΪAC�ӳ�����һ�㣬ED��AB��F��
��1���ж���DCE����״��
��2�����O�İ뾶Ϊ1����OF=![]() ����֤����DCE�ա�OCB��
����֤����DCE�ա�OCB��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������ʽA=9xy��7xy��x��2,B=3xy��5xy��x��7
��1����A��3B;
��2����ҪʹA��3B��ֵ��x��ȡֵ�أ�����y��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������Ӳֿ�O�����ڶ����ֵ�������ˮ�����涨��Ϊ������һ�ε����5�����۵ص�ֱ�ΪA��B��C��D��E�����ص��ֿ�O��������ʻ�ļ�¼����λ��ǧ�ף����£�+2��+3����6����1����2��+4�����ʣ�
��1�����Բֿ�OΪԭ�㣬��Ϊ������ѡ���ʵ��ĵ�λ���ȣ��������ᣬ�����A��B��C��D��E��λ�ã�
��2��������û�������ʻ�˶���ǧ�ף�
��3������������͵�ˮ����100ǧ��Ϊ��������������ǧ������Ϊ�����������ǧ������Ϊ������������A��B��C��D��E����ص��ˮ�������ɼ�Ϊ��+50����15��+25����10����20����û������͵�ˮ���������Ƕ���ǧ�ˣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com