
����Ŀ����1����ͼ�٣���8��6������ͼ�У�ÿ��С�����α߳���Ϊ1��ԭ��O����ABC�Ķ����Ϊ��㣮��C����Ϊ��2��4������OΪλ�����ģ�������ͼ������ABC��ʹ��A��B��C������ABCλ�ƣ���λ�Ʊ�Ϊ1��2����������ͼ�ۼ���
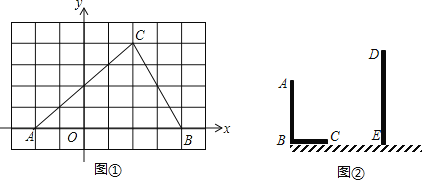
��2�����C��������Ϊ�� ���ܳ���C��A��B��C����C��ABC���� ��
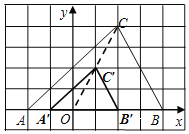
��3����ͼ�ڣ�AB��DE��ֱ���ڵ����ϵ�����������AB��6m��ijһʱ��AB�������µ�ͶӰBC��4m��DE�������µ�ͶӰ��Ϊ6m��
��������ͼ���л�����ʱDE�������µ�ͶӰEF��
�ڸ���������Ϣ���������DE�ij�Ϊ�� m��
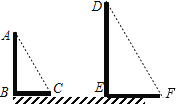
���𰸡���1����ͼ����A��B��C�伴Ϊ�����������Σ�����������2����1��2����1��2����3����ͼ��ʾ��EF����DE��ͶӰ������������DE��9m��
��������
��1������λ��ͼ�ε����ʵó�A����B����C����λ�ã������ó��𰸣�
��2���ɣ�1��������ͼ�οɵã�
��3���ٸ�����֪����AC������D��DF��AC�����ɵó�EF����DE��ͶӰ��
�����������Ρ�ABC�ס�DEF�ó�����ʽ�����DE���ɣ�
�⣺��1����ͼ����A��B��C����Ϊ�����������Σ�
��2���ɣ�1��֪����C��������Ϊ��1��2����
��λ�Ʊ�Ϊ1��2��
���ܳ���C��A��B��C����C��ABC=1��2��
�ʴ�Ϊ����1��2����1��2��
��3��������������AC������D��DF��AC����ֱ��BE��F��
��ͼ��ʾ���߶�EF����DE��ͶӰ��
�ڡ�̫��������ƽ�еģ�
��AC��DF��
���ACB����DFE��
�֡ߡ�ABC����DEF��90����
���ABC�ס�DEF��
��![]() ��
��
��AB��6m��BC��4m��EF��6m��
��![]() ��
��
��DE��9m��
�ʴ�Ϊ��DE��9m��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�κ���y1��kx+n��n��0���ͷ���������y2��![]() ��m��0��x��0����
��m��0��x��0����
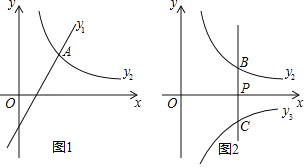
��1����ͼ1����n����2��������������ͼ������A��3��4����
����m��k��ֵ��
��ֱ��д����y1��y2ʱx�ķ�Χ���� ��
��2����ͼ2������P��1��0����y���ƽ����l�뺯��y2��ͼ���ཻ�ڵ�B���뷴��������y3��![]() ��x��0����ͼ���ཻ�ڵ�C��
��x��0����ͼ���ཻ�ڵ�C��
����k��2��ֱ��l�뺯������ͼ���ཻ��D������B��C��D�е�һ�㵽��������ľ������ʱ����m��n��ֵ��
�ڹ���B��x���ƽ�����뺯��y1��ͼ���ཻ���E����m��n��ֵȡ������1������ʵ��ʱ����B��C��ľ������B��E��ľ���֮��dʼ����һ����ֵ�����ʱk��ֵ����ֵd��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+c��a��b��cΪ��������a��0���е�x��y�IJ��ֶ�Ӧֵ���
x | ��1 | 0 | 1 | 3 |
y | ��1 | 3 | 5 | 3 |
���н��ۣ�
��ac��0��
����x��1ʱ��y��ֵ��xֵ���������С��
��3�Ƿ���ax2+��b��1��x+c=0��һ������
������1��x��3ʱ��ax2+��b��1��x+c��0��
������ȷ�Ľ����� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
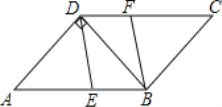
����Ŀ����ͼ����ƽ���ı���![]() �У�
��![]() ��
��![]() ����
����![]() �ڵ�
�ڵ�![]() ����
����![]() �ֱ��DZ�
�ֱ��DZ�![]() �ϵĶ��㣬��
�ϵĶ��㣬��![]() .
.
����֤���ı���![]() ��ƽ���ı��Σ�
��ƽ���ı��Σ�
�ڵ�![]() Ϊ��ֵʱ���ı���
Ϊ��ֵʱ���ı���![]() �Ǿ��Σ�
�Ǿ��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У��Խ���AC��BD�ཻ�ڵ�O��AC��BD�ij���![]() ���Ƿ���
���Ƿ���![]() ��������.��P�ӵ�A��������ÿ��1����λ���ٶ���
��������.��P�ӵ�A��������ÿ��1����λ���ٶ���![]() ��A��O��B��A�ķ����˶����˶�ʱ��Ϊt���룩.
��A��O��B��A�ķ����˶����˶�ʱ��Ϊt���룩.

��1����AC��BD�ij���
��2����APǡ��ƽ��![]() ʱ����P�˶�ʱ��t��ֵ��
ʱ����P�˶�ʱ��t��ֵ��
��3�����˶������У��Ƿ���ڵ�P��ʹ![]() �ǵ��������Σ������ڣ�������˶�ʱ��t��ֵ���������ڣ���˵������.
�ǵ��������Σ������ڣ�������˶�ʱ��t��ֵ���������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijС���ڡ���Ƶ�ʹ��Ƹ��ʡ���ʵ���У�ͳ����ij��Ƶ�ʽ�����ֵ�Ƶ�ʣ���������ͼ��ʾ������ͳ��ͼ����ô������һ�����ʵ�����п��ܵ��ǣ�������

A. ��һö�ʵؾ��ȵ�Ӳ�ң����ʱ����ǡ��������ϡ�
B. ��һ���ʵؾ��ȵ������������ӣ����ʱ���ϵ��������6
C. �ڡ�ʯͷ�������͡�����Ϸ�У�С����������ǡ�������
D. ��������1�������2������ֻ����ɫ�ϵ����𣬴������ȡ��һ�����ǻ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�D��E�ֱ���AC��AB���е㣬CF��AB��ED���ӳ����ڵ�F������AF��CE.
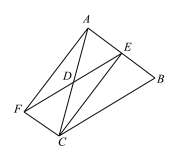
(1)��֤���ı���BCEF��ƽ���ı��Σ�
(2)����ABC����ʲô����ʱ���ı���AECF������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������+��ʱ�������Ϲ��ﱸ��������������ij����ר��һ�����п㣬��ɱ�Ϊÿ��40Ԫ�����ۼ�Ϊÿ��80Ԫʱ��ÿ�¿�����100����Ϊ����������˿ͣ��������ȡ���۴�ʩ�����г����鷴ӳ�����۵���ÿ��1Ԫ����ÿ�¿ɶ�����5������ÿ�����ӵ��ۼ�Ϊ![]() Ԫ(
Ԫ(![]() Ϊ������)��ÿ�µ�������Ϊ
Ϊ������)��ÿ�µ�������Ϊ![]() ����
����
(1)ֱ��д��![]() ��
��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
(2)�������ÿ�»�õ�����Ϊ![]() Ԫ�������۵��۽��Ͷ���Ԫʱ��ÿ�»�õ����������������Ƕ��٣�
Ԫ�������۵��۽��Ͷ���Ԫʱ��ÿ�»�õ����������������Ƕ��٣�
(3)������������Ĺ�����ҵ������ÿ�´������о��200Ԫ����ƶ��ѧ����Ϊ�˱�֤����ÿ��������4220Ԫ�����������ߵõ�����ʵ�ݣ������ȷ�����п�����۵��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
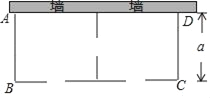
����Ŀ��ijũ��Ҫ��һ����������������ABCD������������һ�濿ǽ��ǽ�����ó���Ϊ27�ף�����������ľ��Χ�ɣ��м�Ҳ��ľ���������ֳ��������أ�������ͼ��ʾ����������1�����ţ�����ľ���������ɺ�ľ���ܳ�57�ף�����������������ABCD���Ŀ�Ϊa�ף�
��1���������ij�Ϊ�����ף��ú�a�Ĵ���ʽ��ʾ����
��2���������������Ϊ288m2����a��ֵ��
��3����aΪ��ֵʱ����������������ʱ�������ﵽ��������Ϊ����ƽ���ף�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com